What is the Difference Between Kinetic Energy and Potential Energy

Introduction:

Energy is the soul of this universe, which drives everything from the motion of celestial bodies to the smallest particles within atoms. It comes in various forms, each with its unique characteristics and behaviors. Two fundamental types of energy, kinetic and potential energy, play vitall roles in understanding the workings of the physical world. In this todays article, I will try to delve into the essence of kinetic and potential energy, exploring their definitions,What is the Difference Between Kinetic Energy and Potential Energy, and their real-world applications.

Explanation:

To start todays article What is the Difference Between Kinetic Energy and Potential Energy, Let us first know What is Kinetic Energy?

Definition of Kinetic Energy:

The energy which is possessed by an object due to its motion is called Kinetic Energy.In another way we can say,In Physics, the energy which is created by the motion of a body is termed as Kinetic Energy.The term "kinetic" originates from the Greek word "kinesis," meaning motion. When an object moves, it carries kinetic energy proportional to its mass and velocity. The greater the mass and velocity of an object, the more kinetic energy it possesses.

Kinetic Energy Formula:

Mathematically, kinetic energy (KE) can be expressed using the following formula:

Kinetic Energy (Eₖ) = ½ mv²

Where, Eₖ = Kinetic Energy of the moving object

m = mass of the moving object

and v = Velocity of the moving body.

This formula illustrates that kinetic energy is directly proportional to both mass and the square of velocity. Therefore, doubling the mass of an object doubles its kinetic energy, while doubling its velocity quadruples its kinetic energy.

Some Real World Instances of Kinetic Energy:

To better understand kinetic energy, let's consider some real-world examples:

Moving Vehicles: A car run down a highway possesses kinetic energy due to its motion. The faster it moves and the heavier it is, the more kinetic energy it carries.

Athletic Activities: A soccer ball kicked into the air or a runner sprinting on a track both exhibit kinetic energy. In these cases, the mass and velocity of the objects contribute to their kinetic energy.

Wind Turbines: Wind turbines transform the kinetic energy of wind into mechanical energy, which is then converted into electrical energy. The rotation of the turbine blades due to wind generates the conversion of kinetic energy into other forms.

Now we will focus on some problems related on Kinetic Kinetic Energy:

Some Problems Related on Kinetic Energy:

Question(1):Work done produced by a force on a moving object is 200J. It was traveling at a speed of 5 m/s. Find the new speed of the object if the mass of the object is 2Kg.

Answer: Here,

work done (w) = 200J

Velocity of the object (u) = 5 ms⁻¹

Mass of the object (m) = 2kg

Let, the new speed of the object = v m/s

As we know that,

∵ We know Work done of a moving object is always equal to its change in kinetic energy

∴ W = ½ m ( v² - u²)

=> 200 = ½ x 2 x ( v² - 5²) [ Putting the values ]

=> 200 = v² - 5²

=> v² = 200 + 25

=> v² = 225

= v = ± 15

∴ New velocity of the object (v) = 15 m [ neglecting -15]

Question(2):A spaceship has a mass of 50000Kg, assume that it travels at 10m/s. Find the kinetic energy possessed by it.

Answer: Here,

Mass of the spaceship (m) = 50000kg

velocity of the spaceship (v) = 10 ms⁻¹

∴ kinetic energy (Eₖ ) possessed by the

spaceship = ½ mv²

= ½ x 50000 x 10² [ Putting values]

= ½ x 50000 x 100

= 50 x 50000

= 2500000 J

= 2500000 /1000 KJ [ ∵ 10³ J = 1 KJ]

= 2500 KJ

Question(3) Assume a ball of 4000Kg by mass was traveling at a speed of 10m/s. Now, this ball transfers all its energy to a ball of mass 10Kg. What will be the velocity of the 10Kg ball after being hit by previous one?

Answer: Here, 1st case

Mass (m) = 4000 kg

velocity(v) = 10 m.s⁻¹

∴ Kinetic energy(Eₖ)= ½ mv²

= ½ x 4000 x 10² [ Putting values]

= 2000 x 100

= 200000 J

2nd case, mass (M) = 10 kg

Let, the velocity of the 2nd ball = V m/s

∵ 1st ball transfers all energy to the 2nd ball

∴ A/Q,

½ MV² = 200000

=> ½ x 10 x V² = 200000

=> 5 x V² = 200000

=> V² = 200000/5

=> V² = 40000

=> V = ± 200

∴ Velocity of the 10kg ball(V) = 200 m/s [neglecting -200]

Now We will know, about Potential Energy

What is Potential Energy?

Explanation of Potential Energy:

Potential energy, unlike kinetic energy, is energy that is stored within an object and has the potential to do work. In anotherway, we can say,The energy which is created by the virtue of change of shape and position of an object by the application of external force is called potential energy.It is often associated with the position or configuration of an object within a force field. The term "potential" suggests that this energy is not actively doing work at the moment but has the potential to do so under the right conditions.

Types of Potential Energy:

Potential energy can manifest in various forms. Some common types include:

Gravitational Potential Energy: This type of potential energy is connected with an object's position concerning the gravitational field. The higher an object is lifted above the ground, the greater its gravitational potential energy.

Elastic Potential Energy: Elastic potential energy is stored in objects like springs, rubber bands, or any elastic material when they are stretched or compressed. It is released when the object returns to its original shape or position.

Chemical Potential Energy: Chemical potential energy is stored within the chemical bonds of substances or compounds. It is released or absorbed during chemical reactions, such as combustion or photosynthesis.

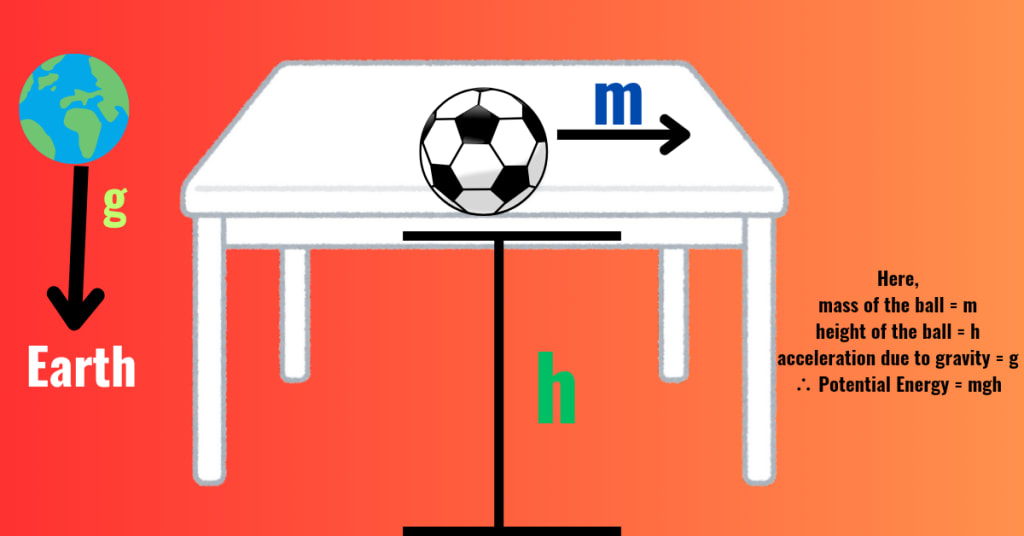
Potential Energy Formula:

The formula for Potential Energy (Ep) is given by Ep=m×g×h

Where ,Ep= Potential Energy

m = Mass of the object

g = Acceleration due to gravity (approximately 9.8 ms⁻² on the surface of the Earth)

h = Height of the object above the ground

This formula shows that Potential Energy is directly proportional to the mass of the object and its height above the reference point.

Real World Examples of Potential Energy:

Let's examine some everyday scenarios that illustrate potential energy:

A Raised Weight: A weight lifted above the ground possesses gravitational potential energy. The higher it is lifted, the more potential energy it has due to its increased height.

A Compressed Spring: When a spring is compressed, it stores elastic potential energy. This energy is released when the spring returns to its original uncompressed position.

Water Behind a Dam: The water stored behind a dam has gravitational potential energy due to its elevation above the ground. This energy can be harnessed to generate electricity through hydroelectric power plants.

Some Problems Related on Potential Energy:

Question(1)A ball of 10Kg is taken from the ground for 20 m up roof of a tall building. The roof makes an angle of 30° with the ground. Find the potential energy of the ball. (Assume g = 10 ms⁻²)

Answer: Let, us assume slant height (l) of the ball = 20 m

Mass of the ball (m) = 10 kg

Angle of elevation (θ )=30°

Acceleration due to gravity(g) = 10 m/s²

Let vertical height of the ball = h m

Again let us assume that the roof is a right triangle

∴ h/l = Sin30°

=> h/20 = ½ [putting values]

=> h = 20/2

=> h = 10

∴ Potential Energy of the ball (Ep) = mgh

= 10 x 10 x 10

= 1000 J

Question(2): A mass of 20Kg is taken from the ground to the height of 50m. Find the potential energy of the object. (Assume g = 10 ms⁻²)

Answer : Here, mass(m) = 20 kg

height (h) = 50 m

acceleration due to gravity(g) = 10 m/s²

Potential energy (Ep) = mgh

= 20 x 10 x 50 J

= 10000 J

Question(3):Find the velocity of the ball just before hitting the ground. Assume that initially, the ball was at a height of 10m from the ground, and its mass was 8Kg. (Assume g = 10 ms⁻²)

Answer: Here, mass (m) = 8kg

height(h) = 10m

g = 10m/s²

Let, the velocity of the ball just before hitting the ground = v m/s

Now,

Potential energy (Ep) = mgh

= 8 x 10 x 10

= 800 J

Initially, at the height of 10m, the ball experiences potential energy. When it is dropped from the up, it starts going towards the ground and its height starts decreasing. With decreasing height, velocity increases, and it acquires kinetic energy.

∴ Kinetic energy (Eₖ) will be = 800J

∴ ½ mv² = 800

=> ½ x 4 x v² = 800

=> 2 x v² = 800

=> v² = 800 / 2

=> v² = 400

=> v =± 20

∴ the velocity of the ball just before hitting the ground (v) = 20 m/s [neglecting -20]

Key Differences between Kinetic Energy and Potential Energy:

As we know both kinetic and potential energy are fundamental concepts in physics, they exhibit distinct characteristics that set them apart:

Nature: Kinetic energy is associated with the motion of an object, while potential energy is related to its position or configuration within a force field.

State: Kinetic energy is active energy, meaning it is being utilized to perform work as the object moves. In contrast, potential energy is stored energy that has the potential to do work under the right conditions.

Formulas: The mathematical expressions for kinetic and potential energy differ. Kinetic energy depends on an object's mass and velocity, while potential energy is influenced by factors such as height, elasticity, or chemical composition.

Conversion: Kinetic energy can be transferred into other forms of energy, such as heat, sound, or electrical energy. Potential energy can similarly be transformed into kinetic energy or other types of energy through various processes.

Representation: Kinetic energy is often represented by the movement or velocity of an object, while potential energy is depicted by the position, height, or configuration of the object within its environment.

To Read more.....