The answer to "Why 1 + 1 = 2?"

Prove that 1+1 does not equal 2

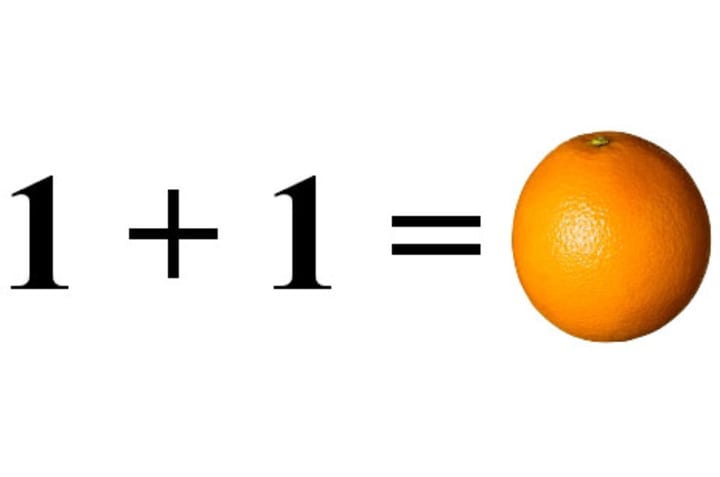
However, from the point of view of modern mathematics, proving "1 + 1 = 2" is redundant, because it does not have any meaning anymore, one can even prove it. that “1 + 1” does not equal 2.

I would like to present to you a construction method in which "1 + 1" will no longer equal 2, but will equal something arbitrary from the point of view of Mathematics.

First of all, we need to have some basic concepts:

1. Gather

This is a basic concept of Mathematics, so we do not have an answer to "What is a set?", but when we talk about Sets, we talk about the objects in it that we call elements. Therefore, we have a way to call a Set according to the properties of the elements in it.

For example: "Set of Natural Numbers" gives us a set whose elements are the numbers 0, 1, 2, 3,...

"The set of vehicles on the road" gives us a set with elements such as cars, motorbikes, bicycles...

People often denote sets with capital letters, such as set A, set B, set of natural numbers N,...

In this article, we will consider an operation on sets called the Cartesian product. Given two sets A and B, the Cartesian product of A and B, denoted AxB, is a set of elements of the form (x; y) in which x is an element of A, y is an element of B (in the same order before and after).

2. Mapping

Given two sets X and Y, a correspondence “each element x of X with only one element y of Y” is called a mapping.

Then, we need to note that in this definition, if x belongs to Y corresponds then it is not called a mapping.

People denote the mapping as f from X and Y, the image of element x belonging to X is denoted as f(x).

3. Build a problem model

After having the above two concepts, let's build a model for the problem that 1 + 1 does not equal 2:

Given the set of natural numbers N and the set of fruit names, denoted T. Then, the Cartesian product of the sets N and N is NxN consisting of elements of the form (a; b) (we call them pairs of numbers (a; b)), where a, b are natural numbers.

Consider the mapping f from set NxN into set T, then, corresponding to each pair of numbers (a; b) is a name of a certain fruit, which is f(a; b). We denote f(a; b) = a + b (note, a + b here is just a symbol).

Then, consider the pair of numbers (1; 1), it will correspond to a certain fruit name in the set T (it must be there according to the mapping definition), let's say it is "Orange". Then we can

f(1; 1) = “Orange”, or in other words, we have “1 + 1 = Orange” (because f(1; 1) = 1 + 1).

4. Conclusion

From the above model, we have the result, 1 + 1 is not 2 anymore, but it can be anything we want. In addition, from this model we also get the answer to "Why 1 + 1 = 2". That is: this is just a convention of mathematical operations set by humans, so humans can completely change it (for example, instead of the "+" sign, people use the "+" sign. -", then we will have "1 - 1 = 2", then essentially nothing has changed, only the symbol has changed).

Looking forward to your feedback!