nCr and nPr

nCr Formula

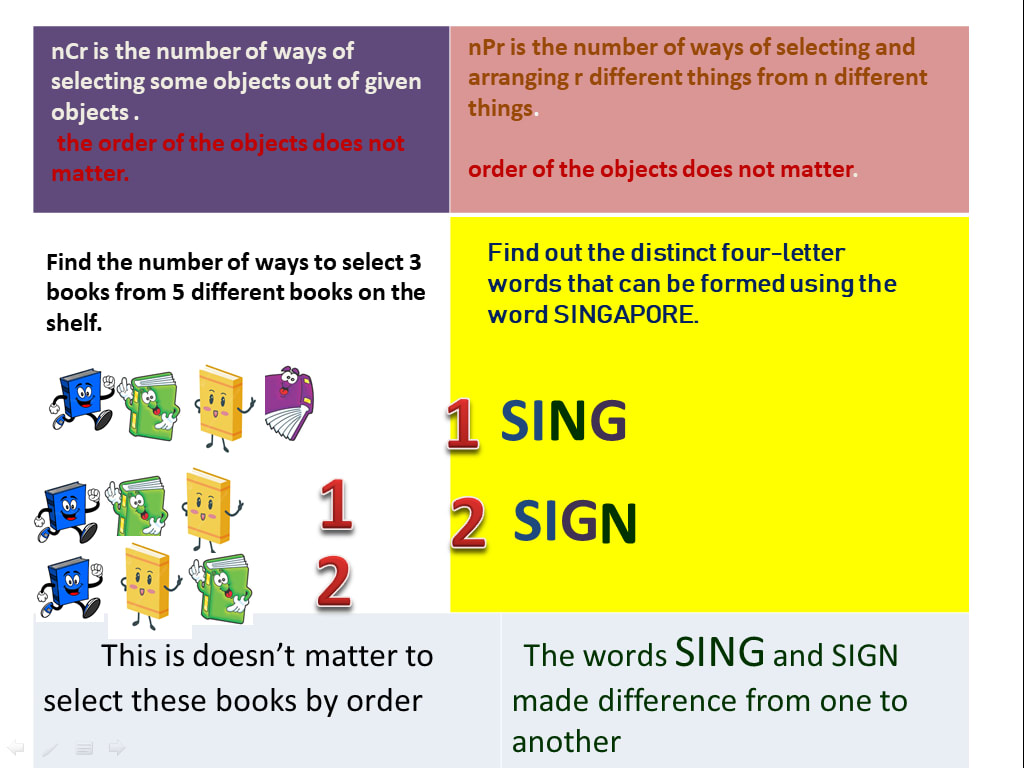
Before going to learn the nCr formula, let us recall what is nCr. nCr is the number of ways of selecting some objects out of given objects where the order of the objects does not matter.

It is expressed as nCr=nPrr!=n!r!(n−r)! It is widely used in probability and statistics.

nCr formula has wide variety of applications in real life as well, like it can be used the number of ways of forming a team or a committee.

Hence it plays vital rule in solving combinatorial problems. Let us learn the nCr formula along with a few solved examples.

What is the nCr Formula?

nCr formula is also known as the "combinations formula". nCr formula is used to find the number of ways of choosing r objects from n objects where the order is not important.

It is represented in the following way.

nCr = 𝑛!/((𝑛−𝑟)! ∗𝑟!)

Here,

• n :- the total number of things.

• r :- the number of things to be chosen out of n things.

☛ Note: nCr is also written as nCr, nCr, C(n, r), (or) nCr.

Derivation of nCr Formula

Let us recap, nPr (or P(n, r) formula, the number of ways to form a permutation of r elements from a total of n can be determined by:

• Forming a combination of r elements out of a total of n in any one of C(n, r) ways
• Ordering these r elements any one of r! ways.

By fundamental counting principle, the number of ways to form a permutation is Using the formula for permutations P(n, r)=n ! /(n-r) ! to substitute into the above formula:

n ! /(n-r) !=C(n, r) × r !

On solving this, the number of combinations, C(n, r)=n ! /[r !(n-r) !].

Examples Using nCr Formula

Example 1: Find the number of ways to select 3 books from 5 different books on the shelf.

Solution:

The total number of books, n = 5.

The number of books to be selected, r = 3.

The number of ways of selecting 3 books out of 5 books is 5C3.

By nCr formula,

5C3 = (5!) / ((5-3)! 3!)

= (120)/(2 × 6)

= 10

☛Check: You may check your answer for 5C3 using the nCr Calculator.

Answer: The number of ways to select 3 books from 5 books is 10.

Example 2: Trevor has to choose 5 marbles from 12 different colored marbles. In how many ways can she choose them?

Solution:

Trevor has to choose 5 out of 12 marbles.

As order doesn't matter here, we use the nCr formula.

n=12

r=5

12C5 = 12!/((12-5)!*5!)

= (12 *11*10*9*8*7!)/(7!*5!)

= (12*11*10*9*8*7!)/(7!*5!)

=(12*11*10*9*8)/(5*4*3*2*1)

= 792

Answer: In 792 ways she can choose the marbles.

Example 3: John asks his daughter to choose 4 pens from the basket. If the basket has 18 different pens to choose from, how many different possible ways she can do it?

Solution:

Given,

r = 4 (sub-set)

n = 18

Therefore, we need to find “18 Choose 4”

Now, Combination = C(n, r)

= n!/r!(n–r)!

= 18!/4!(18−4)!

=18!/14!×4!

= 3,060

Answer: The daughter can choose 4 pens from 18 pens in 3060 ways.

What is nPr Formula?

nPr can be written as P (n, r) (or) n P r (or) n P r.

It is used to find the number of ways of selecting and arranging r different things from n different things.

nPr formula is also known as permutations formula (as we call a way of choosing and arranging things to be a permutation).

This formula involves factorials.

Here is the nPr formula.

nPr = 𝑛!/((𝑛−𝑟)! )

• n = total number of things

• r = number of things that have to be selected and arranged

nPr Formula Derivation

Let us consider n different objects and assume that r different objects from them should be selected and arranged. Let us find a number of possible ways to do this.

• The number of ways of choosing the first object is n as there are n objects in total.

• Since the first object is already chosen, the number of ways of choosing the second object is (n - 1).

• Similarly, the number of ways of choosing the third object is (n - 2).

• While choosing the rth object, there are only (n - r + 1) objects are left and hence it can be chosen in (n - r + 1) ways.

arranging r different objects from n different objects is,

n P r = n (n - 1) (n - 2) ... (n - r + 1)

To simplify this, we use factorial notations. Multiplying and dividing the above expression by (n - r) ... 3 • 2 • 1,

n P r = [n (n - 1) (n - 2) ...(n - r + 1) (n - r) ... 3 • 2 • 1] / [(n - r) ... 3 • 2 • 1]

= n! / (n - r)!

Thus, the nPr formula is derived.

Examples Using nPr Formula

Example 1: Find the value of P(10, 4).

Solution:

Using nPr formula,

P(n, r) = n! / (n - r)!

Substitute n = 10 and r = 4 on both sides,

P(10, 4) = 10! / (10-4)!

= 10! / 6!

= 10 × 9 × 8 × 7 × 6! / 6!

= 5040

Answer: P(10, 4) = 5040.

Example 2: Find the number of 3 letter words that can be formed by rearranging the letters of the word MATH?

Solution:

The number of letters of the word MATH is n = 4.

The number of letters of each of the required words is r = 3.

Since the arrangement matters in the formation of the words, we apply the npr formula to find the required number of 3 letter words.

P(n, r) = n! / (n−r)!

P(4, 3) = 4! / (4−3) = 4! / 1!

= (4 × 3 × 2 × 1) / 1 = 24

Answer: The required number of 3 letter words = 24.

Example 3: 8 students have participated in a running race competition and the top three students will be awarded the first, second, and third prizes. Find the number of ways in which the awarding can be done.

Solution:

The total number of students is n = 8.

The number of students who will be awarded = 3.

Since the arrangement among the first, second, and third prizes matters, we use the nPr formula to find the required number of ways.

P(n, r) = n! / (n−r)!

P(8, 3) = 8! / (8−3)! = 8! / 5!

= (8 × 7 × 6 × 5!) / (5!)

= 8 × 7 × 6

= 336

Answer: The possible number of ways = 336.