Area Of Semi Circle

Introduction:-

The Area Of Semi Circle: Understanding Half the Circle's Beauty

The concept of a circle has influenced mathematicians and thinkers for centuries. Its perfect symmetry, the notion of infinity, and its relationship with various other geometric shapes make it a fundamental element in mathematics and everyday life. One intriguing aspect of a circle is its half, the semi-circle. In this article, I will try to delve into the properties and significance of the semi-circle, focusing on Area of Semi Circle and how it relates to the circle as a whole.

Explanation:-

Defining the Semi-Circle:

Before I explore the Area Of Semi Circle, let's first know its definition. A semi-circle is half of a circle, and it can be formed by cutting a full circle along its diameter. In other words, if we have a circle with radius "r," then the semi-circle would have a radius of "r" and an arc length equal to half the circumference of the full circle.

Now I will start, Today's main topic

The Area of Semi Circle:

To find the Area Of Semi Circle, we can follow a straightforward mathematical process. The formula for the area of a full circle is A = π × r², where "A" represents the area and "r" is the radius of the circle. Since a semi-circle is just half of a full circle, its area would be half of the area of the corresponding full circle.

So, the formula for the area of a semi-circle, which we'll denote as "A_s," is:

A_s = ½ × π × r²

Intuitive Understanding of the Formula:

To develop a more intuitive understanding of the area formula, let's consider a practical example. Let us,Imagine we have a circular garden with a radius of 10 meters. we want to create a walking path that covers half the circumference of the garden while maintaining the same width throughout the path. By cutting the circular garden along the diameter, we'll have a semi-circle with a radius of 10 meters.

Using the formula, we can calculate the area of the semi-circle:

A_s = ½ × π × r² = ½ × 3.14 ×10² [ Let,us assumed π = 3.14] =½ × 3.14 ×100 = ½ × 314 =157 square meters.

This result tells us that the area of the semi-circular path is half the area of the full circular garden. Therefore, the area of the semi-circle is significantly smaller than the area of the whole circle.

Some problems based on Area Of Semi Circle:-

Question(1):-

The diameter of a circle is 14 cm, Find the area of the semi circle.(Take π = 22/7)

Answer :- Here,

diameter of the circle (d) = 14 cm

∴ Radius of the circle (r) = 14/2 = 7 cm

∴ Area of the semi circle = ½ × π × r²

= ½ × 22/7 × 7² [∵ π = 22/7 ]

= ½ × 22/7 × 49

= ½ × 22 × 7

= (11 × 7) cm²

= 77 cm²

Question(2):-

The area of a semi circle is 157 m² Find its diameter.(Take π = 3.14)

Answer:- ∵ Area of the semi circle = 157m²

Let,

Radius of the semi circle = r m

According to question,

½ × π × r² = 157

=> 3.14 × r² = 314

=> r² = 314 / 3.14

=> r² = 31400/314 [Multiplying numerator and denominator by 100]

=> r² = 100

=> r = 10

∴ Diameter of the semi circle = 2 × r

= (2 × 10)

= 20 m

Applications of Semi-Circles:-

The concept of semi-circles also finds applications in various fields, from everyday objects to complex mathematical problems.

Some practical examples are given below:-

(1) Architectural Design:-Semi-circular arches are common in architecture and have been used for centuries in structures like bridges, doorways, and windows. They distribute weight more efficiently and offer increased stability.

(2) Transportation:- The design of roads and highways often involves circular or semi-circular bends to ensure smooth traffic flow and safe navigation.

(3) Geographical and Astronomical Applications:- The semi-circular shape can be seen in natural formations, such as cliffs and valleys, created through erosion or other geological processes. Additionally, the concept of the celestial horizon is related to a semi-circle, dividing the visible sky into two halves.

(4) Trigonometry and Calculus:-In mathematics, the properties of semi-circles are used in trigonometry and calculus to solve various complex problems involving angles, curves, and areas.

(5) Arts and Design:-Artists and designers frequently incorporate the graceful curves of semi-circles in their creations, adding aesthetic appeal and symbolism to their fram works.

Semi-Circles in Mathematics:-

Semi-circles are not only interesting for their visual appeal and practical applications but also for their intriguing mathematical properties. Here are some notable mathematical aspects related to semi-circles:

(1) The Semi-Circular Function: The semi-circular function, denoted as "y = √(r² - x²)," defines the top half of a circle with radius "r" centered at the origin. It is an essential part of trigonometry and calculus, regularly used in solving integrals and differential equations.

(2) Polar Coordinates: In polar coordinates, a semi-circle with radius "r" is represented by the equation "r = a" and α<θ<α+π where, θ = angle ; a and α are constants.This representation simplifies various geometric calculations.

(3) Semi-Circle Theorem: If a right-angled triangle has its hypotenuse as the diameter of a circle, then the triangle is a semi-circle. This theorem is useful in various geometrical proofs and constructions.

This Theorem can be proved as :-

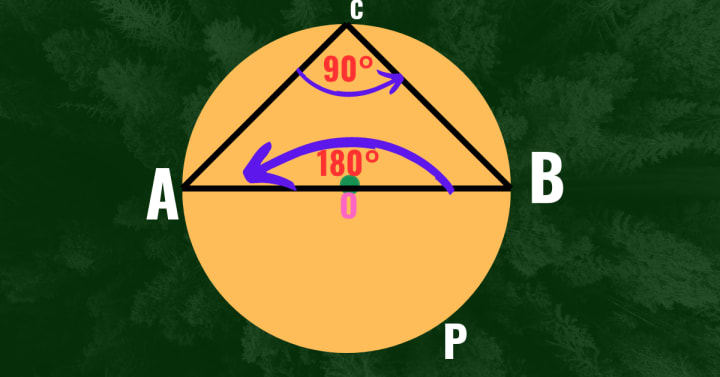
Answer:- Let,

ACB is a right angled triangle ,at C, AB is its hypotenuse is also the diameter of the circle with centre 'O'

To prove :- Δ ACB is a semi-circle.

Proof :- A point P is taken in the circumference of the circle.

∵ <ACB and <AOB are the angles at the circumference and angle in the centre standing on the same arc APB

∴<AOB = 2 × <ACB [ ∵ standing on the same arc angle at the centre is always double the angle at the circumference]

= (2 × 90)°

= 180°

∵ 90° is an inscribed angle of the circle whose centre angle is 180°, So ACB is a semi circle. Hence the right angled triangle ACB is a semi circle. Proved

Conclusion:

The concept of Area of semi-circle, being half of a circle, holds both aesthetic beauty and mathematical significance. Understanding its properties and the formula for its area enriches our knowledge of basic geometry. From architectural marvels to celestial horizons and artistic expressions, semi-circles find numerous applications in our lives.

Lastly if we come across a semi-circle, and take a moment to appreciate its elegance .......

To Read more......