Zipping Through Special Relativity: Reference Frames and Transformations
Einstein's theory of Special Relativity reshaped not just the way we think of physics, but our very concepts of space and time. Here we explore the basics needed to understand Special Relativity.

Even from a modern perspective, it isn't difficult to understand why Einstein's theory of Special Relativity caused such a paradigm shift in physics and science in general. Until its introduction in the 1905 paper, On the electrodynamics of moving bodies, the scientific consensus was that space and time were separate entities—a stage on which the events of the universe played out. Special Relativity would not only unite space and time to a single entity—"Spacetime"—it would also lead to the conclusion that the events of the Universe shape that stage. Spacetime in Space Relativity and later General Relativity was no longer passive, it was a player in the events around it. Einstein proposed that clocks observed to be moving at high speeds would tick more slowly than those at rest.
In addition to this, an object moving at relativistic speeds can be understood to contract along its direction of motion, but not to an observer travelling with it.
These weren't the only revolutionary ideas that SR forced us to accept. Another was the idea of the consistency of the speed of light in a vacuum—denoted c, with a value of roughly 3.0 x 10^8 m/s. Einstein showed that all inertial observers should agree. So intrinsic is this idea to Special Relativity that it became its second postulate. The first postulate is an idea that perhaps wasn't quite so controversial, but lead to important generalisations—the fact that the laws of physics should appear the same to observers in different inertial reference frames.
But before we get to those things, like Einstein, we have to start simply.
As we've now come across the phrase 'inertial reference frame' in many paragraphs it seems like an exploration of this concept is an ideal place to start our journey.
Events and frames of reference
Simply put, an event in spacetime is an occurrence that can be consigned a set of coordinates. In our case, we'll be using traditional cartesian coordinates (x, y, z) for our spatial dimensions. We can assume a frame of reference is a system for assigning coordinates to events. The frame contains a system of synchronized clocks at every point, all of which tick together, thus allowing us to assign a time coordinate (t) to each event, as well as a spatial coordinate.

A frame of reference in two spatial dimensions filled with accurate syncronised clocks. When an event oocurs at a location on the grid it can be assigned a time by a local observer as well as spatial coordinates.
There is a particularly important class of reference frame that is going to be important in the examination of Special Relativity—inertial frames. These are defined as frames of frames in which Newton's First Law of motion holds true. That means essentially reference frames that are moving at constant velocity and not accelerating (as rotation counts as acceleration this means not rotating either).
There's an interesting consequence here. For every inertial frame, there are an infinite amount of such frames moving in constant velocity to this one. The surprising thing about the relationship between these frames is just because one event happens before another in one frame, doesn't mean that these events happen in the same order in all frames!
Introducing our observers, Zip and Zip Prime
These frames would be pretty boring if we left them as is—empty. So we are going to now introduce our inertial observers. Each moves along with their own reference frame. They dedicated to recording events in this frame and only this frame.
Our observers are Zip, a scientist from our Universe who has invented a platform on which he can stand and travel at close to the speed of light without concern for things like friction or energy consumption. The platform also allows Zip to perform all sorts of experiments, which will allow us to test and demonstrate the implications of Special Relativity. Unfortunately for Zip, on one of his first jaunts aboard his platform, he opened a rip in spacetime bringing through his alternate world counterpart, Zip Prime. This, rather egotistical duplicate also has an equally remarkable platform.

Now we've established our inertial frames and our occupiers, we're in a position to see how coordinates transform between these frames. Both at low speeds and then with the adjustments we need to make to these transformations when Zip and Zip Prime are trvelling at speeds comparable to c—the speed of light.
Coordinate transformations and the Lorentz Factor
As the name implies, a theory of relativity is essentially concerned with the relationship between observations made by observers in relative motion. We'll consider Zip's frame S, aligned in what we call 'standard configuration,' with Zip Prime's frame S' (that dash denotes the frame is called S prime, handy as it belongs to Zip Prime). Standard configuration means that the y-axis and z-axis are parallel to the same axis in S' (which we denote y' and z'). The origin (0, 0, 0) of S' travels along the x-axis of S. The relative velocity between the two frames is V. Let's see what that looks like.
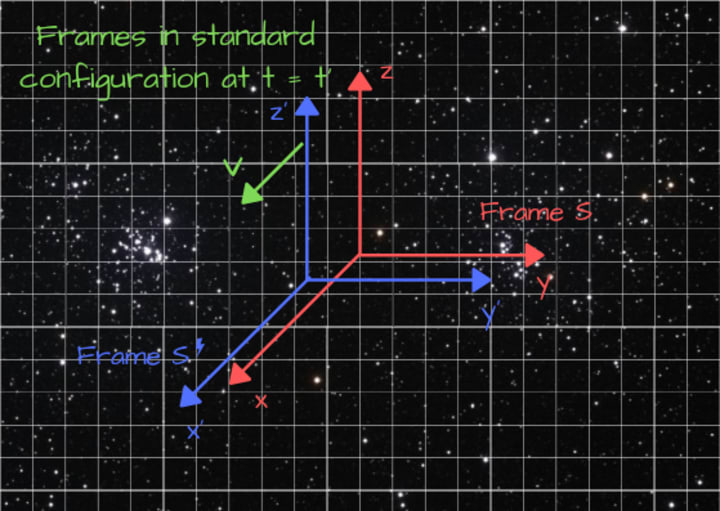
It's pretty easy to see what the transformations will look like for these frames with velocity (V) much slower than c.

The first of these equations implies time is absolute—the time interval between any two events is the same for all observers—something we know that Special Relativity disputes.
Einstein knew he would have to re-postulate these transformation rules if his two postulates, especially the consistency of the speed of light were to hold true. Fortunately, one of his colleagues had already introduced the exact set of transformations that he would need.
The Lorentz Factor—it's electric!
The result that Einstein reached when re-examining the rules of transformation were identical to a set of rules obtained earlier by Dutch physicist Hendrik Lorentz. Lorentz had arrived at these transformations whilst considering James Clerk Maxwell's laws of electromagnetism. This is an important element of the story of relativity and it must have excited Einstein greatly.The whole reason that Einstein began his speculation about the nature of light and the speed at which it travels was a result of Maxwell's laws of electromagnetism—which united the concepts of electricity and magnetism. Maxwell had found that electromagnetic waves travelled at 3.0 x 10^8 m/s—exactly the speed of light. These things, Einstein realised, were no coincidences.The transformations Lorentz found and Einstein capitalised on differ from traditional, as they imply a 'mixing' of time and space as the t' coordinate now depends on x as well as t. The transformations also show that tow observers may not agree on the time of an event—thus meaning time is no longer absolute. You can almost hear physics' sacred cows quivering in fear. The Lorentz transformations themselves look trickier than they are, the key to unpacking them was a little numerical factor that appears all throughout relativity—the Lorentz factor, represented by the Greek letter gamma (γ). This factor is often denoted γ (V) to remind us that it depends on the relative velocity between frames.

For speeds well below that of light (c) the Lorentz factor becomes almost equal to 1 (γ (V) ≈ 1). This means that the Lorentz transformations resemble normal transformations at slow speeds. You can see a graph of that behaviour below.
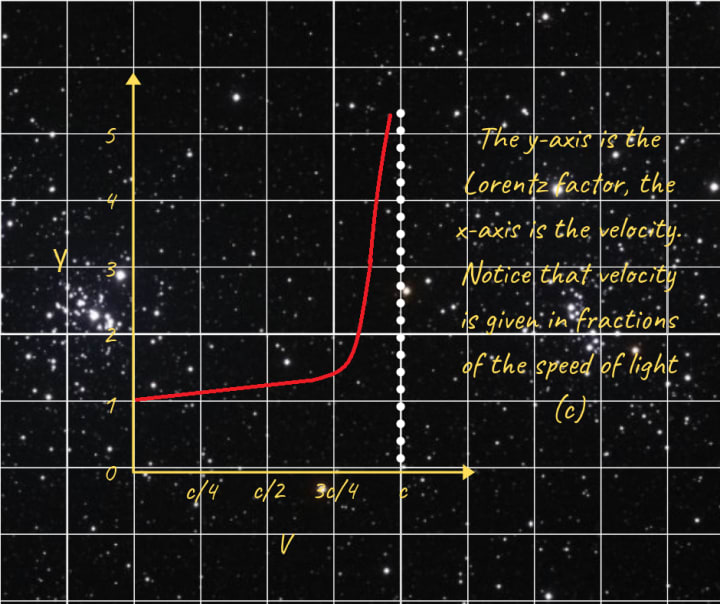
As you can see the Lorentz factor increases exponentially as the speed approaches that of light.
What next?
So, armed with this information and the very basics towards understanding relativity under our belt, where to next? In the next post, we'll examine the incredible of effects of time dilation as Zip and Zip Prime embark on a mission that will take them to neighboring galaxies, only to arrive back to a very different world than they left behind.
Sources and further reading
- Relativity, Gravitation and Cosmology (Lambourne, 2012, Cambridge Press)
- Relativity, Gravitation and Cosmology (Cheng, 2010, Oxford University Press)
- Relativity: A Very Short Introduction (Stannard, 2008, Oxford University Press)
- Special Relativity and Classical Field Theory: A Theoretical Minimum (Susskind, Friedman, 2017, Allen Lane)
About the Creator
Robert Lea
Freelance science writer/journalist. Space. Physics. Astronomy. Quantum physics. Member of the ABSW. Follow me at https://twitter.com/sciencef1rst






Comments
There are no comments for this story
Be the first to respond and start the conversation.