Symmetry and Groups

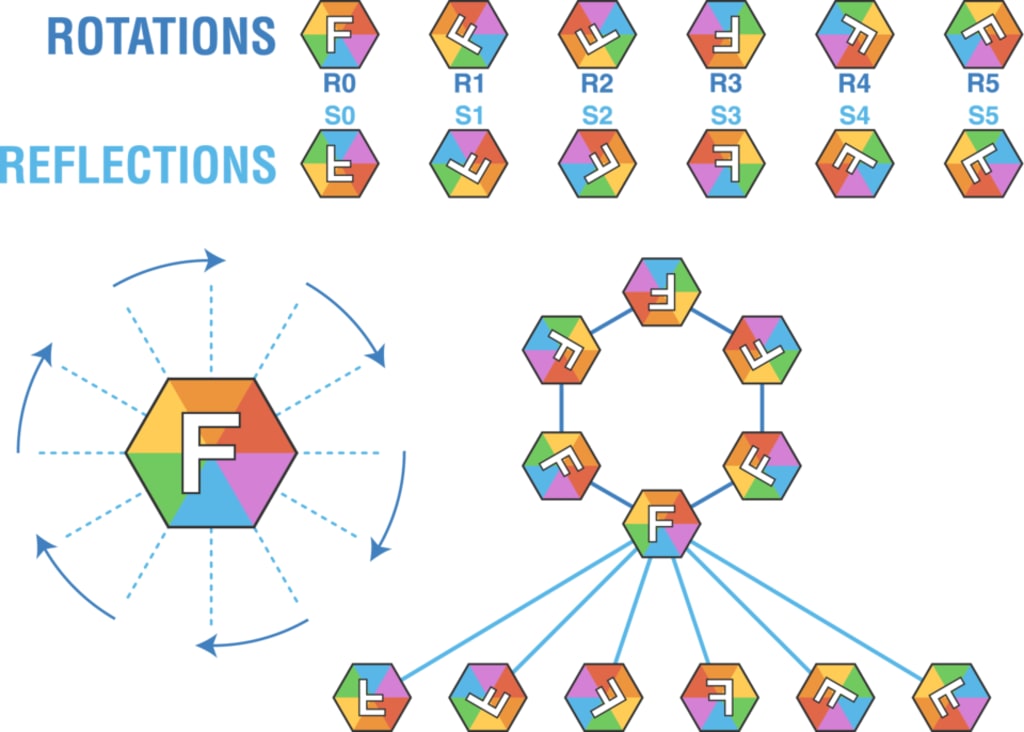
The symmetric group is the group defined over “any set whose elements are all the bijections from the set to itself, and who’s group operation is the composition of functions”, while the symmetry group is “the group of all transformations under which the object is invariant, endowed with the group operation of composition” (Wikipedia) “Isometry” comes from the Greek word for “equal measure”: Isometros. An n-dimensional space in the real numbers has an isometry from one function in R to another. The set of isometries that map a function onto itself on the set of real numbers is called a symmetry group. The symmetry group of an object is dependent on both the object itself and the space in which it is viewed. There are four types of symmetries in two-dimensions: rotation, reflection, translation, and glide reflection. Rotation consists of spinning either left or right. The axis of reflection, or mirror, is the line which acts as a two-way mirror between the original structure and it’s reflection. A translation moves all the points an equal distance in the same direction while a glide-reflection consists of both a translation and a reflection.

Examples of plane symmetry groups number among only the cyclic and dihedral groups. In order to prove the fact that cyclic and dihedral groups are the only finite plane symmetry groups. Given a finite plane symmetry group describing a structure, there can be no translation or glide-reflection, either of which would make the group infinite. The composition between two reflections is a translation because there is no fixed point. By showing that all the elements of the plane symmetry group have a common fixed point, we can claim that the plane symmetry group is a dihedral group.

The set of all possible finite symmetry groups in three dimensions is no more complex than its two dimensional analog. In the pursuit of a system to classify crystalline structures in 1849, August Bravais noticed that there are only three more groups of rotations in three dimensions than in two. The finite groups in three dimensions are the ring of integers modulo n, the dihedral group, A4, S4, and A5. The group of rotations of the solid, G, is made up of six squares and eight triangles. Each square has four rotations that map it onto itself and the rotation group has an order equalling twenty-four, because four rotations times six squares equals twenty-four. (Gallian 461-468)

The degree of symmetry is the number of different symmetry transformations. When there is no symmetry, a system is described as asymmetrical, and a system is any object with respect to its symmetrical properties, or lack thereof. A specific condition that system can find itself in is referred to as a state. Transforming a system from its initial state to its final state is an action that be performed on a system. The inverse of a transformation undoes the effect of another transformation. Rotating something by ninety degrees one direction and then rotating it back ninety degrees is an example of a transformation and an inverse transformation.

The Dodecahedron has a group of symmetries that involve group theory. For any of the given twelve faces of the dodecahedron and the five vertices associated with it, it is possible to move the dodecahedron around the center such that the positions formerly occupied by the face and vertices is now occupied by another side of the dodecahedron. The group consisting of the symmetries of the dodecahedron contains sixty elements reversing orientation and has order one-hundred-twenty. It has twenty rotations of order three about axes joining opposite vertices, in addition to twenty-four rotations of order five, fifteen rotations of pi about axes joining midpoints of opposite edges. All of these symmetries of the dodecahedron are rotations because it is an arbitrary bounded solid. (Foster 1-2).

The dilation transformation, also called a scale transformation, involves changing the lengths of the system to a similar structure: The size of each edge changes with respect to its original size. Temporal displacement, also known as time displacement, displaces a system by an interval of time. (Rosen 62-65). Although they are slightly imperfect, crystal structures are an example of a finite 3-dimensional system that has spacial displacement symmetry. A crystal that is a millimeter across has a total length approximately one million times the minimum displacement interval. Quartz crystals, table salt, ice, rock candy, diamonds, rubies, and sapphires are examples of crystal structures. Crystal lattices can have a rotational symmetry with respect to sets of symmetry axes limited by 2, 3, 4, or 6-fold crystallographic restriction. Crystal latices often have a variety of rotational and reflection symmetries. Crystals are classified by their crystallographic space groups, the two-hundred and thirty independent combinations of symmetries. These crystallographic space groups are separated into thirty-two crystal classes that are separated into seven crystal systems. Astronomical objects that rotate, like Saturn, tend to have only axial symmetry, while those that do not rotate tend to be spherical. Galaxies that rotate eventually flatten into discs with only axial symmetry. Some of these disk-shaped galaxies form a set of arms, changing the type of symmetry from axial to 2-fold. (Rosen 81- 86)

Other examples of symmetric structures in nature are starfish which have 5-fold rotational symmetry and some flowers have rotational symmetry as well. The average snowflake has six-fold rotational symmetry. Carbon atoms arrange themselves into a tetrahedral format where each bond lies along the axis of three-fold rotational symmetry. (Rosen 86). The isometry of the real numbers is one-to-one and its translations form a group. The group of rotations in three dimensions is a 3-prism with equilateral ends that is isomorphic to the dihedral 3-group. Inversion through a point in R3 cannot be realized by rotation in R3. The isometry of a plane preserves angles and an isometry of a plane is completely determined by the image of three non-collinear points (Gallian 467).

“ All scientific applications of symmetry are based on the principle that identical causes produce identical effects” (Rosen 108). Alongside looser definitions of symmetry, Rosen presents a “ The symmetry groups of the cause and effect are indeed mathematical groups. A precise formulation of the symmetry principle is: The symmetry group of the cause is a subgroup of the symmetry group of the effect or coincides with it.” (Rosen 110). Directly applying symmetry to solving a problem is straightforward when the cause is provided. For example, the plane of symmetry of a planet-star system is the plane which passes through the line connecting the centers of both objects. The cause is the combination of the star and planet as well as their instantaneous velocities. “ The effect is the acceleration of the planet” ( Rosen 111). The planet’s instantaneous velocity’s direction is parallel to the plane of symmetry. The planet’s acceleration is parallel to the plane so velocity stays parallel to this plane as well. The planet’s velocity changes direction to the plane of symmetry; the planet’s motion is restricted to the plane of symmetry (Rosen 110-112).

Symmetry can help simplify complex problems in physics. One guideline for constructing a theory that involves symmetry is that the degree of symmetry governing the effect must be higher than the degree of symmetry governing the cause. This is because assuming that the cause has a higher degree of symmetry violates the symmetry principle. One could, however, claim that the effect has a higher degree of symmetry than the cause as long as there is an explanation included as to the reason for this discrepancy. If the cause has a broken symmetry with the ideal symmetry of the effect at the symmetry limit, a theory can be constructed. One interesting example of symmetry in research is that of Erwin Schrodinger applying an equation consistent with special relativity to the hydrogen atom. This experiment was performed before the spin of the electron had been discovered. Although the relativistic equation worked for spinless particles, it is the non-relativistic equation that works for predicting the behavior of the hydrogen atom (Rosen 118-122).

Bibliography:

Foster, Lorraine L. “On the Symmetry Group of the Dodecahedron.” Mathematics Magazine, vol. 63, no. 2, 1990, pp. 106–107. JSTOR, www.jstor.org/stable/2691067.

Joël, N. Leonardo, vol. 13, no. 1, 1980, pp. 71–72. JSTOR, www.jstor.org/stable/1577936

“Chapter 27: Symmetry Groups.” Contemporary Abstract Algebra, by Joseph A. Gallian, Cengage Learning, 2017.

“Symmetry Group.” Wikipedia, Wikimedia Foundation, 9 Dec. 2019, en.wikipedia.org/wiki/Symmetry_group.

“Symmetric Group.” Wikipedia, Wikimedia Foundation, 13 Oct. 2019, en.wikipedia.org/wiki/Symmetric_group.