The 4th Dimension isn’t time

I’m obsessed with the idea of a “dimension”, but there are many misconceptions that the 4th dimension is time. In this article i’m going to go over what 4th dimension actually is, how to make calculations in any dimension and even the 5th dimension.

What is the 4th dimension?

Many people (even mathematicians and physicists) refer to the 4th dimension as time. The only problem is that this goes against our idea of 3-dimensional space. Technically, we live in 4 dimensions, 3 of space and one of time. A 4th dimension is an additional dimension of space, not of time. Someone in the 4th dimension could still experience time the same way that we do.

Before you continue, I’d really appreciate it if you’d consider giving me a follow. Thanks!

The heist

Here is a safe filled with tons of gold, no 2 dimensional creature can access any of this cold because it surrounded by a black safe. When a 2d creature walks up to it, they just see a 2d black square. Despite all that, we can steal this gold, because we can just take the gold from above and the security would have no idea how we took it. They can’t guard the above because they don’t know what “above” is.

Let’s apply this to the 4th dimension now. A 4 dimensional creature, like how we could take the gold from a dimension they don’t know of, could take the yolk from an egg without breaking a shell, a human from a room without opening a door or our money from a safe without opening it. Like how the two dimensional creatures are oblivious to how their precious gold got stolen, we cannot see how our things are stolen, from a dimension that we don’t know of.

In reality, you don’t need to worry about a 4 dimensional creature taking your money (if you were worrying). They couldn’t steal our things simply because we couldn’t exist in their world. Going back to the two dimensional analogy, a 2d creature couldn’t exist in our world because they’d have no height. Even paper has a height, it’s just thin. Something with no height would have no volume and thus wouldn’t exist. In the same way, we couldn’t exist in a 4d world because we would have any “height” in a 4d world. We would have no hyper-volume in their world.

Making squares

Let’s start by looking at the first 3dimensions (1st, 2cd and 3rd).

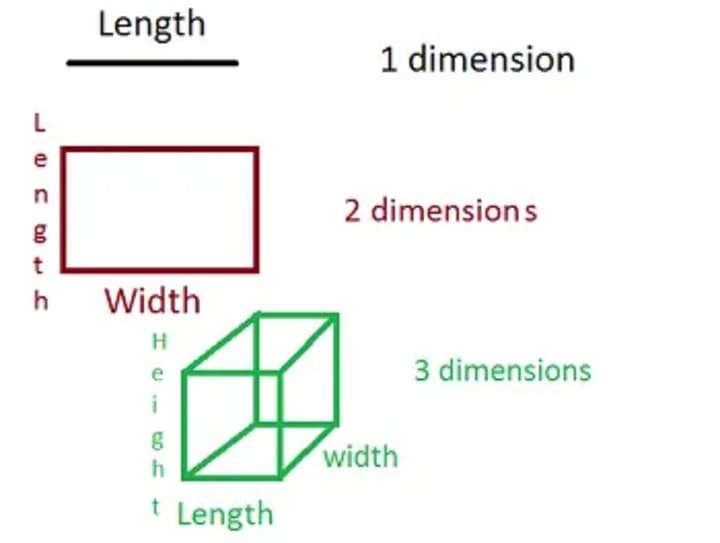
Just as a side note, the 0th dimension (and possibly negative dimensions) do exist, the 0th dimension for instance is a dot, a point with no length and no width. A second side note, a 4 dimensional cube is called a tesseract.

We can calculate the area/volume of a 1-dimensional, 2-dimensional and 3-dimensional “square” (we’re using this term to refer to the shape of all 3).

Assuming that in the diagram length and width (and height) are all the same for each shape and s is the length of each side, the volume of the cube is s³, the area of the square is s² and the length of line is s¹ (s).

This means that for an x-dimensional “square”, the “area” is equal to s^x. So for a four dimensional tesseract, the hyper-volume of the tesseract is s⁴.

Imagine a tesseract as a cube with another line the same way that a square has another line.

Doing these calculations is what helps us grasp the idea of the 4th dimension, we can calculate the hyper-volume of any shape in any dimension which will help us understand them.

Ana and Kata

Howard Hinton coined the terms Ana and Kata. It refers to the 4th dimensional way of moving along the “w” axis. The w axis is the 4th axis on a 4 dimensional graph. North and south for length (y axis), east and west for width (x axis), up and down for height (z axis) and ana and kata for whatever the 4th dimension is (w axis).

Imagine you live in an apartment (maybe you already do and that’s fine). If we lived in a 2d world, we simply say how north or south and how east or west they’d have to go to reach your room. However, us living in a 3d room also tell them how high up (which floor) they’d go to. If we were living in a 4d world, that’s also not enough, now they need to know far ana or kata they need to go.

The Crazy Hypersphere

This part is probably going to be one of the most confusing things I’ve ever written. So, what is a hypersphere? It’s a sphere in higher dimensions and we’re going to look at the 4th dimension for now.

First, a clarification, a sphere is the area around the shape, the ball is the volume in the shape. The surface area of a sphere and the volume of a ball.

Let’s try and grasp the volume of a 4d hyperball. The volume for an n-ball of dimension n, radius r is a terrifying formula:

Let’s break it down. R is the radius and n is the dimension. Γ is the gamma function which represents the factorial. For those unfamiliar, the factorial (n!) is as follows: n! = n * (n-1) * (n-2) … * 2 * 1.

The gamma function allows us to take the factorial of a fraction and is solved through an integral.

1/2 is the most common usage since it has a predictable integration result which turns out to be √π (which is funny and totally unexpected).

A quick note that should be understood is that the gamma of any positive integer n is not n!, it’s (n-1)!.

I’m not going to get too much into the gamma function since it is complicated but just know that it’s usage is for the factorial but for any number.

Back to the hypersphere, let’s fill in the formula, π^(n/2) / Γ(n/2 + 1) * R^n

Let’s fill in the formula and calculate

π^(4/2) / Γ(4/2 + 1) * R⁴

π² R⁴ / Γ(3)

π²R⁴/2!

π²R⁴/2

We get the general formula for a 4d hyperball, π²R⁴/2. If we plugin say, 2 as the radius we get 8π² or ~78.956835 as the hypervolume.

If you though this was confusing, you’re not alone (I did too). But let’s make just a tad bit even more confusing.

The FIFTH dimension???

Theoretically, everything we’ve learnt before also applies here.

For this section, I’ll focus on the idea of the volume of a 5-dimensional hyperball. In case you don’t want to scroll up, this is the formula:

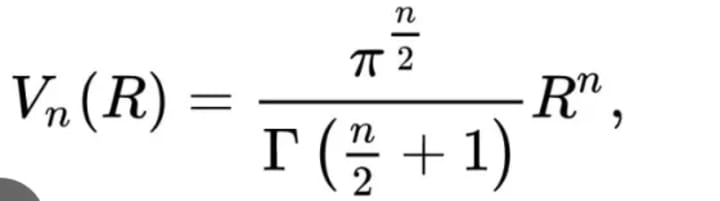
For a hypersphere with radius R and dimension n.

The reason I brought the 5th dimension up is because we’ll finally see the gamma function in play.

We use the same method as last time, plugin and see what happens (sorry about the poor exponent formatting, it’s what Vocal does).

π^(5/2) / Γ(5/2 + 1) * R⁵

π^ 5/2 * / Γ(3.5) * R⁵

Now the gamma of any number n + 1/2 is determined using the following formula:

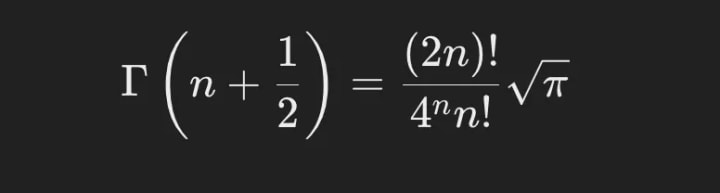
Gamma of n + 1 over 2 = (2n) factorial over 4 to the power of n times n factorial all multiplied by the square root of pi

So let’s fill in this first:

Γ(3 + 1/2) = (2*3)! / 4³*3! * √π

Γ(3.5) = (6)! / 64*6 * √π

Γ(3.5) = 720/ 384 * √π

Γ(3.5) = 15√π / 8

Going back to the original:

π^(5/2) / (15/8 √π) * R⁵

π^(5/2) * (8/ 15√π) * R⁵

8π^(5/2) / 15√π * R⁵

We can rewrite √π as π^(1/2)

8π^(5/2) / 15π^(1/2) * R⁵

We combine the exponents

8π^(5/2–1/2) / 15π * R⁵

8π²R⁵/15π

To be completely honest, this part was just for fun and not at all related to the main topic.

Conclusion

As someone who is still hasn’t graduated high school, I don’t understand every part of what I wrote but I hope this article helped you understand more about the 4th dimension and the wildness of the math behind it.

I’d really appreciate it if you’d consider giving me a follow. Thanks!