Circle theorems:-

Today in this article I will discuss on circle theorems which are for school going students of class 9 and class 10

Prove that perpendicular drawn from the center of a circle intersect a chord bisects the chord.

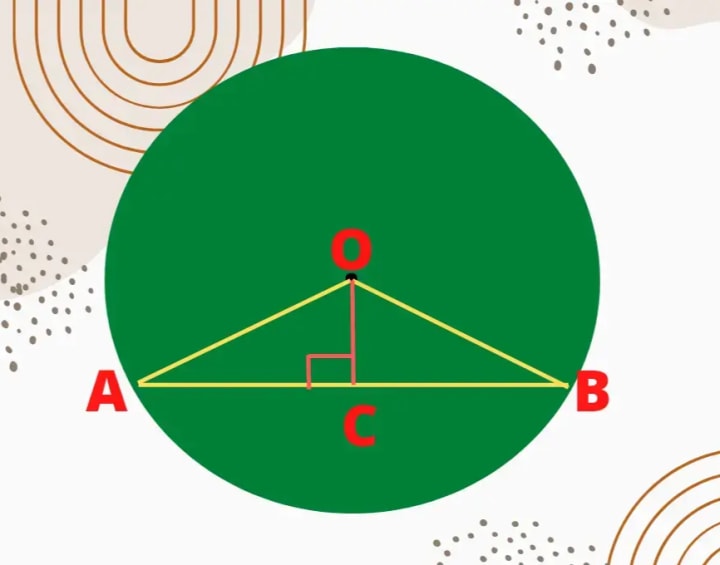
Answer:-

In the picture, a circle is drawn with center 'O' AB is a chord of the circle. Perpendicular drawn from the center 'O' on the chord AB. i.e; OC⊥ AB

To prove that:- OC bisects AB,i.e; AC = BC

Construction:- OA and OB are drawn.

Proof:- In between Δs AOC and BOC we get,

∵ OA = OB [ ∵ radii of the same circle]

∵ OC = OC [ ∵ Common side of the Δs]

∵ ∠OCA = ∠OCB [ ∵ both are 90°]

∴ Δ AOC ≌ Δ BOC [ By SAS congruence rule of the Δs]

∴ AC = BC [∵ By CPCT] Proved

Prove that line joining the midpoint of a chord of a circle bisects the chord is perpendicular on the chord.

Prove that line joining the midpoint of a chord of a circle bisects the chord is perpendicular on the chord.

Answer:-

In the picture, AB is a chord of a circle with center 'O' C is the midpoint of AB , OC is joined which bisects AB at point 'C' i.e; AC = BC …..(1)

To prove:- OC ⊥ AB

Construction:- OA and OB are joined.

Proof:- In between Δs AOC and BOC we get,

∵ OC = OC [∵ Common side of the Δs]

∵ AC = BC [∵ from (1)]

and OA = OB [∵ radii of the same circle]

∴ Δ AOC ≌ Δ BOC [∵ By SSS congruence rule of the Δs]

∴ ∠ OCA = <OCB [ by CPCT] but they are adjacent angles.

∴ ∠OCA = <OCB = 180°/2 = 90°

∴ OC⊥ AB Proved.

Prove that, angle at the center of a circle is double the angle of the circumference standing on the same arc of the circle.

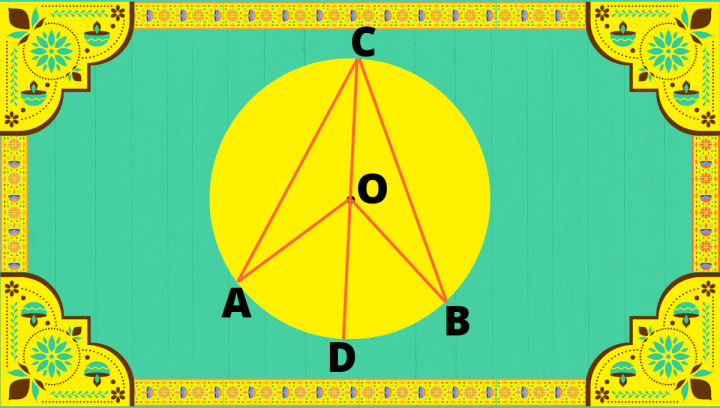
Answer:-

In picture, <AOB and <ACB are the angles at the center and at the circumference respectively,standing on the same arc ADC of a circle with center 'O'

To prove that:- <AOB = 2<ACB

Construction:- OC is joined and extended upto D.

Proof:-

∵ In Δ AOC, we get

∵ OA = OC [ ∵radii of the same

circle]

∴ ∠OCA = <OAC…..(1) [∵angles opposite to the equal sides are also equal]

Again,

In Δ AOC

∵ <AOD = <OCA + <OAC [ ∵ sum of two remote interrior angles of a Δ is equal to exterrior angle]

=> <AOD = <OCA+<OCA [using (1) ]

=> <AOD = 2<OCA …..(2)

Similarly we can prove,

<BOD = 2<OCB ……..(3)

Now,

(2)+(3) we get,

<AOD+<BOD = 2(<OCA + <OCB)

=> <AOB = 2<ACB Proved.

Prove that equal chords of a circle are equidistant from the center.

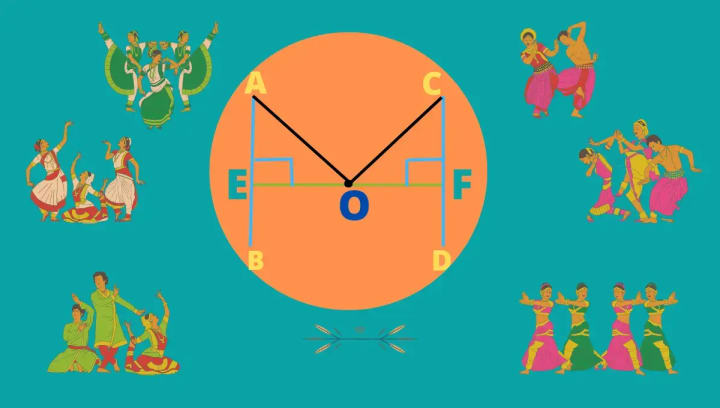
Answer:-

In the picture , AB and CD are two chords of a circle with center 'O' also AB=CD,and

OE⊥AB, OF⊥CD ,To prove:- OE=OF

Construction;- OA and OC are joined.

Proof:-

∵ OE⊥ AB

∴ AE = ½ AB [∵ ⊥ drawn from the center on the chord bisects the chord]

Similarly,

CF= ½ CD

∵ AB = CD [∵Given]

=>½ AB = ½ CD [∵dividing both sides by2

=>AE = CF

Now in between Δs OAE and OCF we get,

∵ AE =CF [∵ Proved]

∵ OA = OC [∵ radii of the same circle]

and, <OEA = <OFC [∵both are 90°]

∴ ΔOAE ≌ ΔOCF[∵by SAS rule of congruence of Δs]

∴ OE= OF [by CPCT]

Proved.

Prove that equidistant chords of a circle are equal.

Answer:-

In the picture , AB and CD are two chords of a circle with center 'O' OE⊥AB, OF⊥CD, also OE = OF, To prove:- AB=CD

Construction:- OA and OC are joined.

Proof:- ∵ OE⊥ AB

∴ AE = ½ AB [∵⊥ drawn from the center of a circle on a chord bisects the chord]

Similarly,

CF = ½ CD

Now in between Δs OEA and OFC we get,

To read.........more

https://bit.ly/3duECSU