A Classic Clock Problem in Math for your entertainment

I will never forget my 5th and 6th-grade Math teacher. He was stout, stern, and strict in discipline. Being one of the few male teachers in school, students with discipline issues often ended up seeing him. Even though corporal punishment had been outlawed, he always carried with him a thick wooden ruler, and all students knew that ruler was not just for drawing straight lines on the blackboard. Because of his high standard of ‘law and order’, many students were scared of him.

But that is not all I remember about him. Seemingly cold and unfriendly, he was actually a very passionate math teacher and had impacted me a lot.

As I grew up, all my other Math teachers focused on teaching me how to ‘do Math’, on the contrary, my 5th and 6th-grade Math teacher had shown me how to think. To him, Math is all about thinking hard and deep, not remembering formulae and proofs. He always made Math fun and challenging to learn; many of the math problems that he went over in class could not be found in a standard Math curriculum. Every Friday, he gave students tricky problems to work on over the weekend and I always looked forward to Monday to see which classmates managed to find a solution. He had seeded a genuine love of math inside of me and I am forever grateful to him.

In this article, I will go over one of the problems he assigned in class — the ‘clock hands’ problem. It is a fun and easy math problem for elementary or middle schoolers, if you have children at home you may enjoy going over it with them.

The problem:

A clock face has two hands, the hour hand, and the minute hand. The former moves slower, and the latter moves faster. Every hour, say between 4 o’clock and 5 o’clock as an example, the two hands will have a chance to overlap once, find the exact time when it happens.

A modified version of the problem is:

Every hour, say between 4 o’clock and 5 o’clock, the two hands will have at least one chance to form a right angle, find the exact time when it happens.

The solution:

Well, you can take out a clock and find the answers by actually moving the hands on the clock face, but it is fun to do it mathematically.

First, take note that a clock face has 60 equally spaced tick marks, and we know the speed of the movement of each hand is:

Relative speed is a fancy term for the difference between the speed of the two hands. It quantifies the amount by which the separation between the two hands will be shortened as every minute passes.

At 4 o’clock, the hour hand is at 4 and the minute hand is at 12, which means there is an initial separation of 20 tick marks between them. Since the minute hand moves faster, as time passes this separation will decrease until it is down to zero. To calculate how long it takes for that to happen, we shall make use of the relative speed:

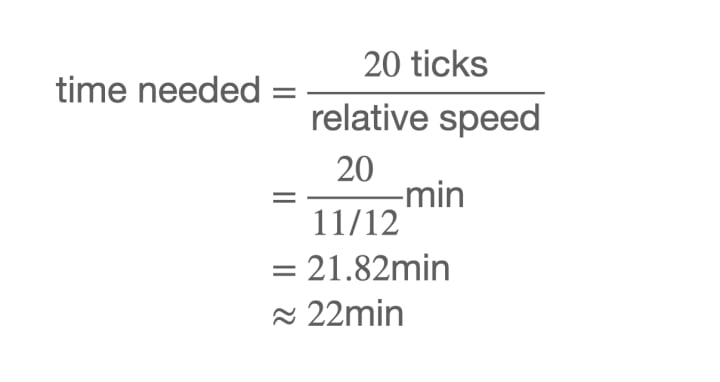
In other words, the two hands will overlap at about 4:22, as shown in the picture.

To find the exact times when the two hands form a right angle is more tricky since it can occur when either the minute or the hour hand leads by 15 tick marks, and sometimes 45 tick marks depending on the hour.

From 4 o’clock to 5 o’clock, the first time the two hands form a right angle is when the hour hand leads by 15 ticks. Since their initial separation is 20 ticks, the minute hand only needs to shorten their separation by (20–15) ticks, therefore

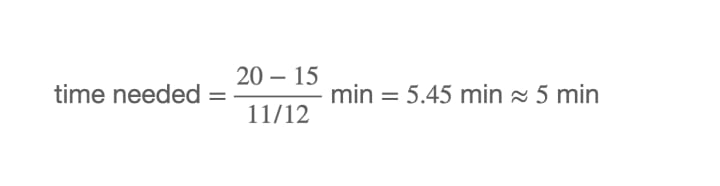
This means at around 4:05 the two hands first form a right angle.

The second time it occurs when the minute hand manages to lead another 15 ticks after overlapping with the hour hand. The time needed is

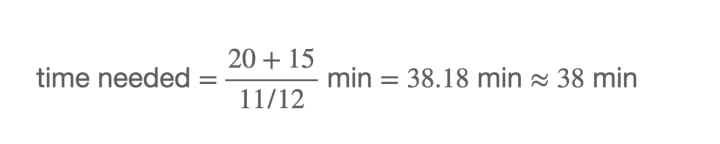
See these pictures for yourself:

I know children these days prefer digital clocks more than analog ones, but it is still fun to teach them how to handle classic math problems related to the clock face. With a real clock at hand, they can verify the answer right away and feel accomplished, like how I felt when I was young.

These are the times, correct to the nearest minute, at which the two hands overlap, one is different from the next by about 1 hour and 5.45 minutes(prove it yourself!):

12:00 1:05

2:11 3:16

4:22 5:27

6:33 7:38

8:44 9:49

10:55

These are the times, correct to the nearest minute, at which the two hands form a right angle:

12:16 12:49

1:22 1:55

2:27

3:00 3:33

4:05 4:38

5:11 5:44

6:16 6:49

7:22 7:55

8:27

9:00 9:33

10:05 10:38

11:11 11:44

Enjoy playing with your old clock!

This article was first published on Medium, here is the link.