Trigonometry Formulas

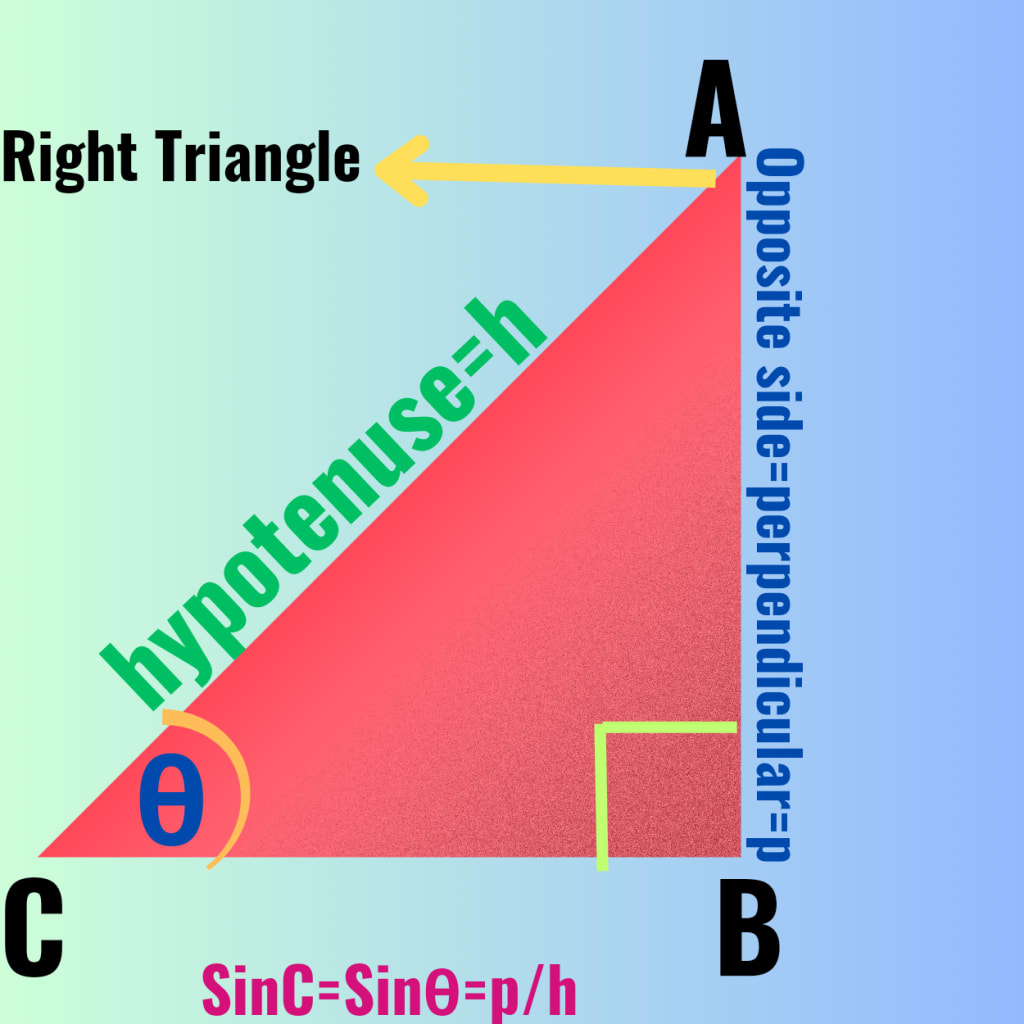
Introduction:

Trigonometry, a branch of mathematics that deals with the relationships between the sides and angles of triangles, has been a fundamental part of mathematical knowledge for centuries. Trigonometry Formulas play a crucial role in solving various mathematical problems, particularly those involving angles and distances. In this comprehensive guide, I will try to delve into the essential Trigonometry Formulas, their applications, and how they contribute to solving real-world problems.

Explanation:

To start today’s article Trigonometry Formulas Let us first know, some key basic concepts of trigonometry.

Basic Trigonometric Ratios:

Trigonometry revolves around six primary trigonometric ratios, which are based on the sides of a right-angled triangle. These ratios are sine (sin), cosine (cos), tangent (tan), cosecant (csc), secant (sec), and cotangent (cot). Let's explore each of them:

Sine (sinθ):

The sine of an angle in a right-angled triangle is the ratio of the length of the side opposite the angle to the length of the hypotenuse for an angle θ

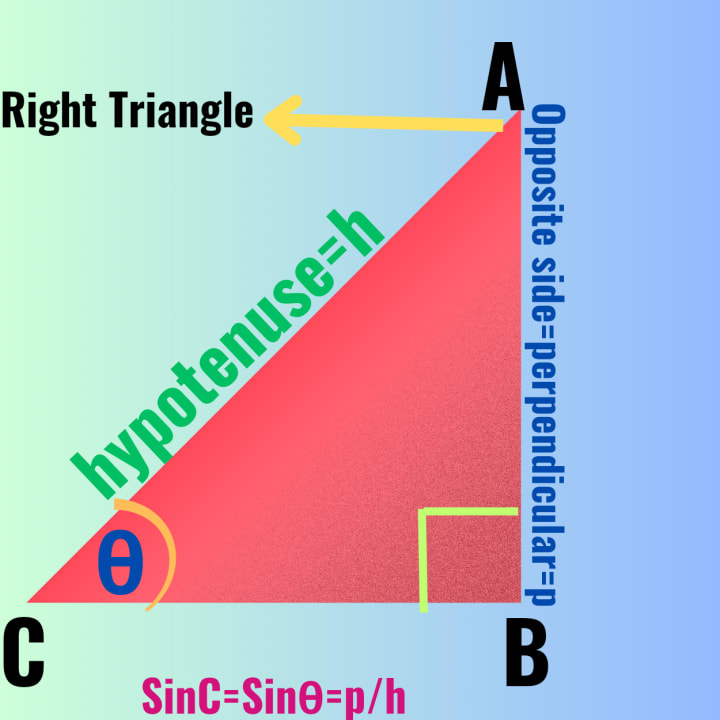
Sinθ = Opposite side of ∠θ / hypotenuse,which can be expressed as,

Sinθ = p/h, where p = perpendicular and h = hypotenuse of the right triangle.

Cosine (cosθ):

The cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse for an angle θ

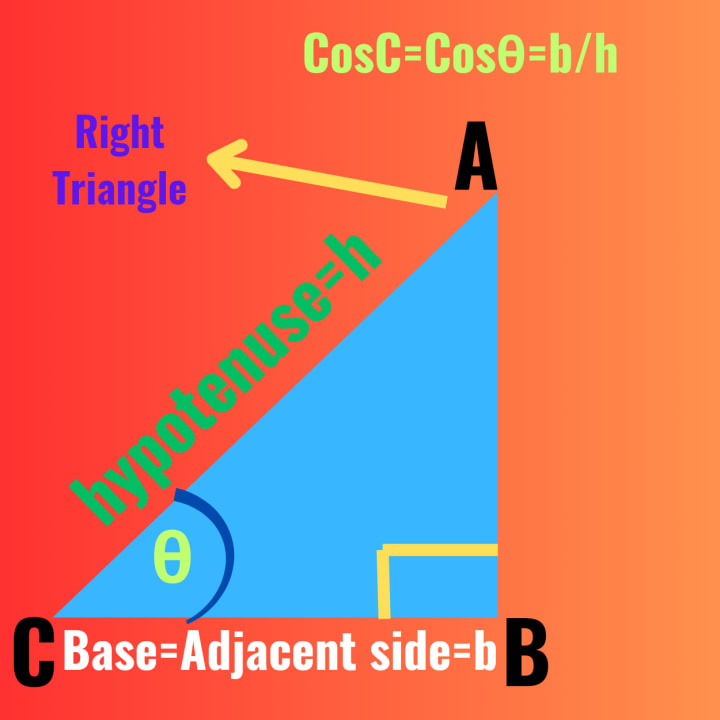
cosθ = Adjacent side of ∠θ /hypotenuse which can be also expressed,

Cosθ = b/h, where b = base and h = hypotenus of the right triangle.

Tangent (tanθ):

The tangent of an angle is the ratio of the length of the side opposite the angle to the length of the adjacent side for an angle θ

tanθ = Opposite side of ∠θ/ Adjacent side which can be also expressed,

tanθ = p/b, where p = Perpendicular and b = base of the right triangle.

Cosecant (cosecθ):

The cosecant of an angle is the reciprocal of the sine.

cosecθ =1/sinθ

Secant (secθ):

The secant of an angle is the reciprocal of the cosine.

secθ =1/cosθ

Cotangent (cotθ):

The cotangent of an angle is the reciprocal of the tangent.

cotθ =1/tanθ

Pythagorean Identities:

The Pythagorean identities are fundamental trigonometric relationships derived from the Pythagorean theorem. They are expressed as equations involving the sides of a right-angled triangle.

Pythagorean Theorem:

The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse (h) is equal to the sum of the squares of the lengths of the other two sides base(b) and perpendicular(p),which is written as,

h² = p² + b²

Pythagorean Identity:

The Pythagorean identity is derived from the Pythagorean theorem and is expressed in terms of trigonometric functions.

sin²α + cos²α = 1

Prove that: sin²α + cos²α = 1

Answer:

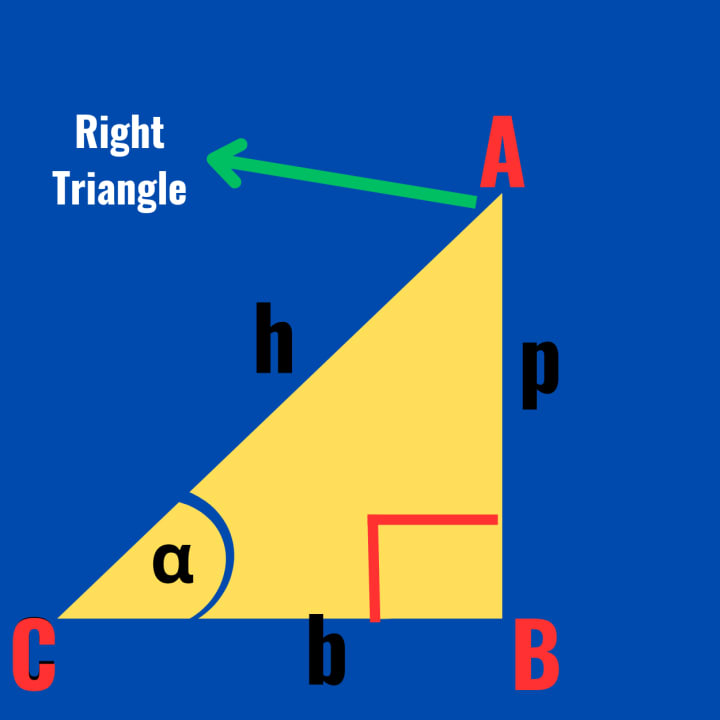
Let, ABC is a right angled triangle at B

whose, hypotenuse = AC = h

base = BC = b

perpendicular = AB = p

and ∠C = α (Let, us say)

To prove : sin²α + cos²α = 1

Proof:-

∵ ABC is a right angle triangle at B,then according to pythagoras Theorem, we get

∴ AB² + BC² = AC² [ ∵ < B = 90°]

=>AB²/AC² + BC² /AC² = AC² / AC²

[ ∵ dividing both sides by AC² ]

=>( p/h)² + ( b/h)² = 1

=> Sin²α + cos²α = 1 Proved.

This identity holds true for all angles and is a foundational relationship in trigonometry.

Reciprocal Identities:

Reciprocal identities are derived by taking the reciprocals of the basic trigonometric ratios.

sinα = 1/cosecα

cosecα = 1/ sinα

cosα = 1/ secα

secα =1/cosα

tanα =1/cotα

Co-function Identities:

Co-function identities are expressed in the relationship between the trigonometric functions of complementary angles (angles that add up to 90 degrees).

1. Sine and Cosine:

sin(π/2 - θ) = cosθ

cos(π/2 - θ) =sinθ, where θ is an acute angle.

2.Tangent and Cotangent:

tan(π/2 - θ) = cotθ

cot(π/2 - θ) = tanθ, where θ is an acute angle.

3. Secant and Cosecant:

sec(π/2 - θ) = cosecθ

cosec(π/2 - θ) = sec(π/2 - θ),where θ is an acute angle.

Double-Angle and Half-Angle Formulas:

Double-angle and half-angle formulas are used to express trigonometric functions of angles that are twice or half of a given angle θ or β any one we can assume.

1. Double-Angle Formulas:

sin(2θ) = 2sinθcosθ

cos(2θ) = cos²θ - sin²θ

tan(2θ) = 2 tanθ / (1- tan²θ),where θ is an unknown angle.

2. Half-Angle Formulas:

sin (β/2) = ± √(1-cosβ) /2

cos (β/2) = ± √(1+cosβ) /2

tan(β/2) = ± √(1-cosβ) /(1+cosβ)

Sum and Difference Formulas:

Sum and difference formulas allow the expressions of trigonometric functions of the sum or difference of two angles in terms of the trigonometric functions of the angles themselves.

1. Sum Formulas:

sin(x +y)=sinxcosy + cosxsiny

cos(x +y)=cosxcosy − sinxsiny

tan(x +y)= (tanx + tany) /(1- tanxtany),

where x and y are two different or may be similar angles.

2. Difference Formulas:

sin⁡(x−y)=sin⁡xcos⁡y − cos⁡xsin⁡y

cos(x−y)=cosxcosy + sinxsiny

tan(x−y)= (tanx - tany) /(1+tanx.tany)

where x and y are two different or may be similar angles.

Other Identities of Trigonometry:

1. Sec²θ -Tan²θ = 1

2. Cosec² - Cot²θ =1

Some Problems of trigonometry formulas:

Question(1): Prove that, (Cosecθ - Cotθ)² = (1 - Cosθ) / (1+ Cosθ)

Answer:

L.H.S = (Cosecθ - Cotθ)²

= (1/ Sinθ - Cosθ/Sinθ)² [ using trigonometry formulas]

= {(1 - Cosθ) /Sinθ}²

= (1 - Cosθ)² / Sin²θ

= (1 - Cosθ)(1 - Cosθ) / (1- Cos²θ)[using trigonometry formula]

= (1 - Cosθ)(1 - Cosθ) / {(1)² - (Cosθ)²}

= (1 - Cosθ)(1 - Cosθ) /(1 - Cosθ)(1 + Cosθ)

[ using formula,a² - b² = ( a - b)(a+b)

= (1 - Cosθ) /(1 + Cosθ)

= R.H.S Proved.

Question(2): Prove that, (1 + Sec A) / SecA = Sin²A / 1 - CosA

Answer: L.H.S = (1 + Sec A) / SecA

= (1+1/CosA) ÷(1/ CosA)

= {(CosA + 1) / CosA} x CosA

= CosA(CosA + 1) / CosA

= (CosA + 1) / 1

= (1+ CosA ) (1- CosA) / 1- CosA [Multiplying numerator and denominator by (1- CosA)]

= (1 - Cos²A) / 1- CosA [ Applying (a+b)(a-b) =a² - b²]

= Sin²A / 1- CosA [using trigonometry formula]

= R.H.S Proved

Question(3): Show that, 1/(1+Sinθ) +1/(1-Sinθ) = 2Sec²θ

Answer: L.H.S = 1/(1+Sinθ) +1/(1-Sinθ)

= (1-Sinθ +1+Sinθ) /(1+Sinθ)(1-Sinθ)

= 2 /(1- Sin²θ)[Applying (a+b)(a-b) =a² - b²]

= 2 / Cos²θ [Using trigonometry formula,Cos²θ =1- Sin²θ]

= 2 x 1/Cos²θ

= 2 Sec²θ [ Using reciprocal formula]

= R.H.S Showed.

To Read more....