The Laurent Phenomenon and Somos Sequences

The Laurent Phenomenon is a general phenomenon which has also special cases in which “Laurentness” is involved. Their introductory theorem states: “In a cluster algebra of geometric type, each cluster variable can be expressed as a Laurent polynomial with integer coefficients in the elements of any extended cluster” [1]

Cluster algebras are “constructively defined commutative rings equipped with a distinguished set of generators (cluster variables) grouped into overlapping subsets (clusters) of the same finite cardinality (the rank of an algebra in question)”. Cluster algebras have a feature called seed mutations which consist of a seed which is a pair (x,b). Getting to the seed in the first place is sort of confusing and requires understanding of terms which are new to me, such as “exchange relations” and “skew-symmetrizable”. Once you have the seed, there is an iteration of the clusters which consists of a matrix mutation which gives you the seed mutation in a particular direction. [2]

Wolfram Mathworld describes the Somos sequence as "a set of related symmetrical recurrence relations which, surprisingly, always give integers. The Somos sequence of order k, or Somos-k sequence” [3]

~Introduction~

When it has constants as coefficients, the fourth-order quadratic recurrence relation describes the Somos 4 sequences. Some Somos 4 sequences have been explained using the Laurent Phenomenon. Cluster algebras have been use to prove that that the these types of recurrences are actually the same as the fundamental cases of the Laurent Phenomenon. The comparison between Somos 4 sequences and the elliptic curve points sequences indicate that the two are the same. [4]

In “Perfect Matchings and The Octahedron Recurrence,” Speyer discusses the a three-dimensional lattice and proves that the values of the recurrence on it are Laurent polynomials. The proof in this paper generalizes Aztec Diamonds which Speyer states are: “graphs whose perfect matching have extremely structured combinatorics and soon formed their own, second line of research as other graphs were discovered with the similar regularities.” The paper goes on to provide a deeper description of what Aztec Diamonds are. [5]

~The Laurent Phenomenon~

Overview: A Laurent series is a delineation of a complex function as a power series with the variable's positive and negative powers.

The Laurent Phenomenon refers to the behavior of the series. The Laurent series analyzes complex functions in areas which have poles or other points where the function is undefined or infinite. The Laurent phenomenon arises when a function has an isolated singularity at its core.

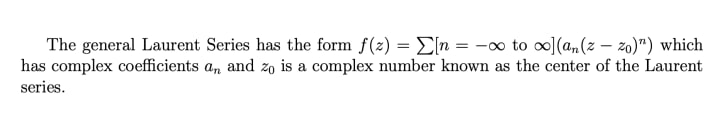
The value of the coefficients of the Laurent series determine how the function will behave about the pole or singularity. The Laurent phenomenon takes place when the series includes infinitely many terms which have negative powers.

About this point, the function oscillates. [6]

Theorems: The Laurent Phenomenon includes several different examples: the cube recurrence, the Gale-Robinson sequence, Octahedron recurrencce, the two-term version of the Gale-Robinson sequence, the Caterpillar lemma, generalized Somos 4 sequence, the knight recurrence, number walls, Burchnall-Chaundy polynomials, and monic palindromic polynomials in one variable. [6]

~Somos Sequences~

History: The Somos sequence is a recursive integer-based sequence. It has applications in combinatorics and algebraic geometry. The Somos Sequence has an initial set of values which are which are usually positive and its recursive formula. It was found by Michael Somos in 1989. The formula for the Somos sequence is shown in another section and each term is a linear combination of products of the previous terms divided by another previous term. Some Somos sequences are related to integrable systems in algebraic geometry and some can provide integer solutions in diophantine equations as opposed to fractional solutions which are generated by other sequences. Michael Somos is an American mathematician who came up with Somos sequences while working on theta functions. Theta functions are made up of several complex variables and are present in abelian varieties, moduli spaces, quandratic forms and solitons. The theory of elliptic functions includes theta functions. [7]

Polynomial Somos Sequences: The following algebraic characteristics of the Somos sequence for Somos-k sequences are described by Bykovskii and Romanov in 2021 in the paper "Polynomial Somos Sequences":

The Riordan Array, the A-matrix, and Somos-4 sequence: Riordan arrays have A-matrices and rho-sequences. Paul Barry conjectured that "The form of a generic A-matrix leads to Somos 4 sequences". Riordan arrays have sequence characterization, which means that a lower-triangluar array is Riordan if and only if there exists a sequence which is a finite sum. The matrix rho is the production matrix of the Riordan matrix M. A matrix characterization can be used to reach the sequence catergorization of the Riordan array. The production matrix rho of a Riordan array is unique but the pair (A, rho) may not necessarily be. There is set of the Riordan arrays that is a subgroup of the Riordan group and is called the subgroup of Bell matrices. The binomial matrix, also known as Pascal's triange is a type of Riordan array. There are a few examples using these elements: Motzkin triangle defined by the Riordan array, the Riordan array derived from a Bell subgroup element, the fact that Somos 4 sequences and Riordan arrays are sequences that are closely related to elliptic curves. What is the relationship between A-matrices and Somos conjectures? The A-Matrix can be expanded to give a sequence to which the Hankel transform is applied, giving the Somos 4 sequence. The Bell matrix has an A-matrix which is actually the Riordan array. [9]

Heron triangles and Somos 5 Sequences: When a triangle has side lengths of integer length and an internal area which is also an area, this is called a Heron triangle. Reiterating this concept but where the length of the sides are rational numbers and the area is a rational number as well, we get version of a Heron triangle. When all three medians of the triangle are rational, then the triangle is considered "perfect". It has been conjectured that these sorts of triangles do not exist, however Buchholz and Rathburn proved that there is an infinite number of Heron triangles that have only two medians which are rational. This infinite subset is associated with the rational points on an elliptic curve and Buchholz and Rathburn also found a connection to Somos 5 sequences with a specific formula for the integer side lengths of the triangle, the two rational medians, and the areas which exist in this infinite family of Heron triangles. The proof includes using Somos-5 sequences and Quispel-Roberts-Thompson maps in the plane using complex analysis and real dynamics. [10]

Somos 4,6, and 8 Sequences: There are families of integer sequences which have Hankel transforms turn out to be Somos 4 sequences, Somos 6 sequences, and Somos 8 sequences. We can describe these sequences in terms of Riordan arrays which are streched to the Catalan numbers with a Hankel transform accompanying. The Hankel transform and the theory of Jacobi fractions and orthogonal polynomials have been used to derive Somos sequences. [11]

~Laurent Phenomenon and Somos Sequences~

Propp and Fomin and Zelivinsky previously studied this recurrence which is defined on a three dimenional lattice with Speyer proves that each coefficient is equal to one. Fomin and Zelivinsky made the original tie to the Laurent Phenomenon and guessed that the terms had all the coefficients of one. Somos tried to rebuild Theta functions in a combinatorial manner.

Although Somos was able to find that all of the coefficients of Laurent polynomial were non-negative, he failed to prove it and this proof is the topic here.

The Gale-Robinson recurrence can be considered a special case of the Octahedron Recurrence. Essentially, we will end up finding that with any initial conditions, with a specified different initial conditions than usually used. When the Gale-Robinson recurrence is reduced to the octahedron recurrence, some of the the initial conditions of the octahedron recurrence are equal to other initial conditions of the octahedron recurrence, so a lot of the monomials which would have been distinct if the initial conditions of the octahedron recurrence had not been altered are in fact the same as the monomials of the Gale-Robinson recurrence. The purpose of this paper was to show that "all of the coefficients of the Laurent polynomials computed by the Gale-Robinson recurrence are positive."[12]

R-Systems: The field of geometric crystals and geometric Robinson-Schensted-Knuth correspondence led to using birational toggling on Gelfand-Tsetlin patterns. Birational rowmotion, which is a discrete dynamical system, was introduced and is associated with a partially ordered set. If birational rowmotion is generalized to the group of arbitrarly strongly connected directed graphs. Galashin and Pavlo Pylyavskyy study the integrability using singularity confinement and algebraic entropy to show that the singularity confinement in the R-system can reduce into a Laurent phenomenon in a cluster algebra or Laurent phenomena algebra which leads to various sequences with interesting symmetries and some of those are Somos and Gale-Robinson. [13]

~Bibliography~

[1] Fomin , Sergey, et al. Introduction to Cluster Algebras. Harvard University, 2020.

[2] LeClerc, Bernard, and Lauren K. Williams. Cluster Algebras | PNAS, www.pnas.org/doi/10.1073/pnas.1410635111. Accessed 22 May 2023.

[3] https://mathworld.wolfram.com/SomosSequence.html

[4] Integrality and the Laurent Phenomenon for Somos 4 Sequences, arxiv.org/pdf/math/0508094v3.pdf. Accessed 22 May 2023.

[5] Speyer, David E. “Perfect Matchings and the Octahedron Recurrence.” arXiv.Org, 2 Mar. 2004, arxiv.org/abs/math/0402452.

[6] Fomin, Sergey, and Andrei Zelevinsky. “The Laurent Phenomenon.” arXiv.Org, 25 Apr. 2001, arxiv.org/abs/math/0104241.

[7] “Somos Sequence.” Wikipedia, 18 Nov. 2022, en.wikipedia.org/wiki/Somos_sequence.

[8] Bykovskii, V. A., and M. A. Romanov. “Polynomial Somos Sequences - Functional Analysis and Its Applications.” SpringerLink, 8 Sept. 2021, link.springer.com/article/10.1134/S0016266321010020.

[9] Barry, Paul. “Riordan Arrays, the A-Matrix, and Somos 4 Sequences.” arXiv.Org, 2 Dec. 2019, arxiv.org/abs/1912.01126.

[10] Hone, Andrew N. W. “Heron Triangles with Two Rational Medians and Somos-5 Sequences.” arXiv.Org, 18 Sept. 2022, arxiv.org/abs/2107.03197.

[11]Barry, Paul. “Conjectures on Somos 4, 6 and 8 Sequences Using Riordan Arrays and the Catalan Numbers.” arXiv.Org, 22 Nov. 2022, arxiv.org/abs/2211.12637.

[12]Speyer, David E. “Perfect Matchings and the Octahedron Recurrence.” arXiv.Org, 2 Mar. 2004, arxiv.org/abs/math/0402452.

[13]Galashin, Pavel, and Pablo Pylyavskyy. “ArXiv:1709.00578v1 [Math.CO] 2 Sep 2017.” R-Systems, arxiv.org/pdf/1709.00578.pdf. Accessed 22 May 2023.