Rock, Paper, Scissors: Nature's Playful Strategy.

Almost everybody learns the two-player “Rock, Paper, Scissors” game quite early on in life - but beyond being just a bit of fun, or perhaps a means to determine whose turn it is to take the trash out - were you aware that this simple game also embodies a strategy that plays an important role in the evolution of life and the maintenance of biodiversity?

Rock, Paper, Scissors is an ancient game whose origins seem to date back at least to the beginning of the common era. In an early Japanese version of the game shown in the figure above, the thumb, the little finger and the index finger were used as hand symbols, but the principle was the same as the modern version of the game in which we use a fist to denote rock, a flat hand to denote paper, and a v-shaped index and second finger to denote scissors. Following the simultaneous showing of hands by the two players, the winner is determined as follows: if rock and paper are shown, paper wins (paper wraps rock), if rock and scissors are shown, rock wins (rock blunts scissors), and if paper and scissors are shown, scissors wins (scissors cut paper). Any time that both players show the same symbol, the result is declared a draw.

In this relationship between the three possible symbols, paper beats rock, rock beats scissors, and scissors beat paper, so that there is no surefire strategy to win. Any pure strategy such as “always play scissors” can easily be beaten by an opponent adapting their strategy to your own - in this case, switching to “always play rock”. The same is true for any mixed strategies in which each symbol is played a certain fraction of the time. There is always an adaptation that the opponent can make in order to favor winning over losing. In the end then, neither player is able to get the upper hand simply by switching their own strategy and in formal game theory terms, this kind of inflexion point scenario represents the Nash Equilibrium for the Rock, Paper, Scissors game.

As ancient as the Rock, Paper Scissors game is, like many things that we humans claim to have invented, it turns out that nature beat us to the punch. Different bacterial strains that are able to coexist within a particular ecosystem, have actually been playing this game for a few billion years. The Escherichia coli bacteria that are the major commensal bacteria in the digestive tracts of warm-blooded animals (including humans) provide a perfect example of an evolutionary Rock, Paper, Scissors strategy that can actually promote and maintain biodiversity in a bacterial ecosystem.

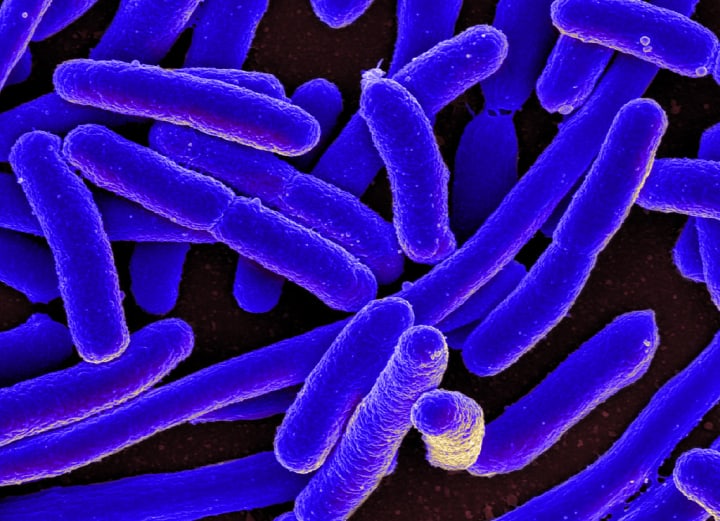
Imagine an ecosystem in which initially, only a “wild-type” E. coli strain is present - adapted to its particular environment but otherwise free of any selection pressure from competing strains of bacteria. Then - into the wild-type E. coli’s perfect world, comes a new strain of the bacteria that’s definitely playing to win with a nasty new strategy that threatens the very existence of the wild-type strain. These new guys produce an antibiotic called colicin that is toxic for E. coli - but in order to take advantage of this new weapon, the colicin-producing strain must also develop resistance to its own poison in order not to shoot itself in the proverbial foot while it’s in the process of poisoning its competitors.

This colicin-producing strain does however pay a price for the acquisition of these new weapons. In addition to some fraction of the more general metabolic activities that enable the cell to thrive being diverted to the production of the antibiotic - being resistant to its own antibiotic also requires it to be more selective in the ways that it absorbs nutrients from the environment. Via their combined, detrimental effects on the colicin-producing strain’s ability to grow and reproduce, both of these factors compromise the bacteria’s reproductive rate in comparison with the wild-type strain. The slow reproductive rate of the colicin-producing strain would normally place it at a significant disadvantage to the faster-growing wild-type strain, but for the fact that it is now armed with the ability to kill off its competitor (and also to survive its own attack).

The resources of any ecosystem (such as nutrients) are finite, so in general, the increased presence of any particular strain means that there are less resources for another strain. If the colicin-producing strain is able to reduce the population of the wild-type strain through the production of its antibiotic, it frees up more of the ecosystem’s resources for its own growth

At this point, you might be thinking it’s game over for the wild-type strain since it has no resistance to the antibiotic of the colicin-producing strain, and will inevitably die out - but then something very interesting happens …

The presence of the antibiotic in the environment starts to favor the selection of wild-type strains that bear mutations conferring resistance to the antibiotic, and in time, antibiotic-resistant strains evolve from the wild-type population. An antibiotic-resistant strain does not produce the antibiotic itself, but it does have to make some of the same metabolic compromises as the colicin-producing strain in order to overcome the antibiotic’s toxicity. As a result, the resistant strain of E. coli, like the colicin-producing strain, is unable to grow and reproduce as rapidly as the wild-type bacteria - but since it does not have to actually produce the colicin antibiotic, it is able to grow and reproduce faster than the colicin-producing strain.

In a head-to-head competitive race for survival, the wild-type strain of E. coli cannot survive in the presence of the antibiotic from the colicin-producing strain, which eventually out-competes the wild-type and displaces it entirely from the ecosystem. In a race between the resistant and colicin-producing strains, the resistant strain is perfectly capable of surviving the antibiotic, and since it also grows and reproduces faster than the colicin-producing strain, it eventually out-competes and displaces it. In a race between the wild-type and resistant strains, the resistant strain poses no threat to the wild-type since it does not produce the antibiotic to which it has developed resistance. Absent the presence of the antibiotic in the environment therefore, the resistant strain has no advantage at all, and is in fact, it at a disadvantage relative to the wild-type since it grows and reproduces more slowly.

And this is where it gets really interesting …

When these three strains of bacteria grow in a well-mixed solution such as stirred bacterial culture, the resistant strain always end up displacing the other two strains. This occurs because the colicin-producing strain eventually kills off all of the wild-type with its antibiotic, thereby setting up the head-to-head competition between the resistant and colicin-producing strains that we know the resistant strain will always win.

When these three strains of bacteria grow on a surface however, the ability of the resistant strain to survive in proximity to the colicin-producing strain, creates areas in which there is no antibiotic being produced, and in which the wild-type can survive. The wild-type strain therefore, is dependent upon the presence of the resistant strain for its survival. In its turn, the presence of the rapidly-growing wild-type keeps the resistant strain in check since per capita, it consumes resources at a greater rate than the resistant strain. If the wild-type were not present, this would set up a head-to-head competition between the colicin-producing strain and the resistant strain, which we know the resistant strain would always win. The colicin-producing strain therefore depends for its survival upon the ability of the wild-type strain to keep the resistant strain in check. Similarly - the resistant strain depends upon the colicin-producing strain to keep the wild-type strain in check and avoid the head-to-head competition with the wild-type strain that it would inevitably lose.

You can see where this is going …

• The wild-type strain beats the resistant strain
• the resistant strain beats the colicin-producing strain
• the colicin-producing strain beats the wild-type strain

Rock - Paper - Scissors

In this three-way competition, any Darwinian notion of “survival of the fittest” is thrown out of the window in favor of a kind of cooperative coexistence. If any one of the three strains were to proliferate too strongly, this would create the conditions in which it would be placed in direct competition with the strain against which it would have no chance of survival. It is therefore not in the best interests of any of the strains, to aggressively outcompete the others, and what arises from this situation is a kind of cooperative equilibrium that actually promotes biodiversity within the ecosystem.

Experiments that demonstrate this cooperative behavior between bacterial species, have been done in the laboratory, but an easier way to demonstrate it - one that does not require a laboratory and bacterial cultures - is to use a computer simulation. A few years ago, a collaborative group of scientists at Stanford and Yale universities published a series of rock, paper, scissors experiments with three strains of bacteria, accompanied by just such a simulation, but alas they did not provide any details on how the algorithm for the computational simulation was implemented, nor any code. They did however publish the details of the lattice simulation algorithm that they used, and armed with this, I decided to reproduce their simulation using one of my favorite coding languages, Python.

In the Python code, the lattice-based ecosystem is implemented as a two-dimensional, square grid with periodic boundary conditions applied (topologically equivalent to a torus), and I used a grid dimension of 250 locations for each axis, in order to follow the conditions used in the article. The stochastic simulation algorithm itself runs as follows:

Populate the entire grid randomly with equal probabilities at each location for the wild-type (antibiotic-sensitive) strain (s), the colicin-producing strain (c), the colicin-resistant strain (r), or an empty location.

Cycle the grid through n generations, as follows:

For each grid location:

If the location is empty, it is populated according to a set of weighted probabilities proportional to the occupancy of each strain at the eight neighboring locations

If the location is occupied, the strain that is present is randomly killed according to a fixed probability for the r and c strains, or a base probability for the s strain multiplied by a toxicity factor proportional to the fractional occupancy of c strains in the neighboring locations

Rinse and repeat

With periodic boundary conditions applied to the grid, the neighborhood of each location wraps around the axes, so that a location at the end of an axis is also adjacent to one at the beginning of that same axis and so on. Following the first step of the algorithm, the initial grid contains a roughly even mix of s, c and r strains, as well as empty locations, that looks something like this:

In the images and in the simulation videos below, I am using the following color scheme: the wild-type s strain is shown in green, the colicin-producing c strain is shown in red, the antibiotic-resistant r strain is shown in orange, and empty locations are shown in white.

The parameters that govern the dynamic behavior of this mixed population over the course of the simulation are:

p(c): the probability of death of the colicin-producing strain

p(r): the probability of death of the resistant strain

p(s): the probability of death of the wild-type strain,

toxicity: the multiplying factor for p(s) based upon the fractional occupancy of the colicin-producing strain in the neighboring locations

The neighboring locations can be defined in one of two ways. For any given location on the grid, the local neighborhood consists of the eight adjacent locations, whereas the global neighborhood consists of the entire grid. The reason to implement a global neighborhood option is to allow the simulation to represent the well-mixed state, where for example, all three strains are in a stirred, liquid cell culture. As we will see when we look at the simulation results - under the same set of rules and parameters, the populations of bacteria behave very differently when they are growing on a surface and sampling their local environments, versus when they are growing in a well-mixed culture in which they are effectively sampling their global environment.

So let’s first look at a simulation in which the three strains of bacteria are growing on a surface and sampling only their local environments. In the video below, you can follow the evolution of the bacterial population on the grid, over 5000 generations, with a snapshot of the population having been taken every 100 generations. The parameters used in the simulation are shown above the population grid, and the color scheme for the three strains is as described above.

The first thing you probably noticed is that the initially random distribution of bacteria on the grid quickly evolves into a more macroscopic pattern of patches as the three different strains of bacteria become spatially partitioned - in fact, once this pattern of spatial partitioning is established, it endures for the rest of the simulation. The actual locations of the patches of the three strains may change, but the overall appearance of the population is remarkably stable. In the bottom left corner of the simulation, the fractional occupancy of each strain on the grid is reported, as well as the fraction of empty locations. The fraction of empty locations remains stable at about 1/3 once the initial, spatial partitioning has occurred, with the three bacterial strains sharing the remaining 2/3 of the grid. The relative quantities of each strain may change over the course of the simulation but overall, you can see that they coexist remarkably well, with no one strain ever really becoming dominant.

This simulation represents the Rock, Paper, Scissors scenario discussed above, in which each strain in this non-transitive community competes within its own local neighborhood, and the dynamics of the population dictate that it is not in the best interests of any one strain to become too dominant. The three bacterial strains coexist quite nicely and the population diversity is maintained.

Now let’s look at what happens if we keep all of the simulation parameters exactly the same, but switch to global sampling instead of local sampling - effectively mimicking the scenario in which the bacteria are in a well-mixed liquid culture.

Here’s what that simulation looks like:

Well that was short!

As you can see, when the bacterial population is well-mixed (as it would be in a liquid cell culture), the wild-type strain dies off almost immediately, the colicin-producing strain is then very rapidly overtaken by the colicin-resistant strain, and by about the 400th generation, only the colicin-resistant strain is left - exactly what is observed in the laboratory. In the well-mixed population, the wild-type strain cannot avoid exposure to the antibiotic, and once it dies out, the superior growth and reproduction rate of the resistant strain makes it an inevitable winner over the more slowly growing colicin-producing strain.

One of the great things about computer simulations like this, is that you can do virtual experiments with them - for example, let’s take a look at how the presence of the antibiotic from the colicin-producing strain affects the diversity of the bacterial population on the grid. If we lower the toxicity parameter to say 0.35, we can effectively represent the situation in which we have an attenuated colicin-producing strain that is producing less antibiotic (or a less effective antibiotic).

Here’s the simulation for reduced levels of antibiotic.

Interestingly, the first casualty of lower levels of antibiotic is the resistant strain. This might seem a little counterintuitive at first, but if you think back to our earlier discussion about the rock, paper, scissors relationship between the three bacterial strains, you will recall that the resistant strain depends upon the presence of the colicin-producing strain to keep the faster-growing wild-type strain in check.

Once all the resistant strain has died out by about the 300th generation, the simulation becomes a head-to-head competition with the fast-growing wild-type and the attenuated colicin-producing strain. In this scenario, a non-attenuated colicin-producing strain would progressively dominate the population grid and eventually displace the wild-type altogether - but while the attenuated strain is able to hold its own locally, it is clear that at this lower level of antibiotic, it is slowly losing the battle with the wild-type strain. Like the brave Spartans at Thermopylae, the colicin-producing bacteria hold on by a thread in their small enclave, until finally being overrun by the wild-type strain at about generation 3800. The remaining tiny population of colicin-producing bacteria are living on a knife edge of stability prior to their final extinction, their fortunes fluctuating with the stochasticity of the population dynamics.

It is clear from these simulations, that somewhat counterintuitively, the presence of significant levels of antibiotic actually promotes biodiversity, even paradoxically ensuring the survival of the strain that it was designed to poison. This last simulation illustrates very well the decrease in biodiversity that results from a significant loss in the activity of the colicin-producing strain.

Theoretical models have predicted that even competing species are able to coexist within an ecosystem when they can only interact with one another on a small, local scale, i.e. with their nearest neighbors. This scenario has also been shown to apply particularly when the competing species are part of a non-transitive community - that is, they do not participate in competitive hierarchies. These theoretical models also predict that the biodiversity of such communities is lost when the competing species are able to interact with one another over larger scales - in the case of bacteria in a well-stirred liquid culture for example.

The lattice-based, stochastic simulations presented in this article, mirror the predictions of these theoretical models, as well as reproducing what has been observed empirically in the laboratory. They also serve as a nice demonstration of the ability of computational modeling and simulation to help us understand the dynamic behaviors of biological systems.

© Gordon Webster - Gordon is a partner at the digital biology research firm Amber Biology, a Ronin Scholar, and co-author of Python For The Life Sciences.